Australian Mathematics Competition - 2010 - Upper Primary - Grade 5 & 6 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesWhat is one thousand and twenty-seven in numerals?
(A) 100027
(B) 10027
(C) 1027
(D) 127
(E) 27
Jillian is standing inside a pet shop and looking out the window shown in the diagram.

Lee is 14 years old. Liz is 10 years old. Dad's age is twice the sum of their ages. How old is Dad?
(A) 46
(B) 48
(C) 50
(D) 52
(E) 54

The midpoints of the sides of a square are joined as shown. A part of the original square is shaded as shown. What fraction of the original square is shaded?
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{6}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{1}{3}\)
(E) \(\frac{1}{5}\)
In a queue in the school canteen, Sarah was behind Tim and Carl was between Sarah and Tim. Sarah was in front of Brett who was in front of George. Who was fourth in line?
(A) Sarah
(B) Tim
(C) Carl
(D) Brett
(E) George
When five numbers are added the total is 2010 . One of the numbers is changed from 235 to 532 . What is the total of the five numbers now?
(A) 1723
(B) 2542
(C) 2360
(D) 1896
(E) 2307
Eight blocks are glued together as shown.

What is the difference between the largest and smallest 3-digit numbers that can be made from the following 1-digit cards, if each card is to be used once only in each number?

(A) 477
(B) 495
(C) 1009
(D) 468
(E) 555
My father won \(\$ 1000\) in a lottery. He put one-fifth in the bank, spent one-quarter of what was left on me and gave the rest to my mother. How much did my mother receive?
(A) \(\$ 400\)
(B) \(\$ 888\)
(C) \(\$ 450\)
(D) \(\$ 550\)
(E) \(\$ 600\)

Starting at \(A\) and walking around the figure back to \(A\), how far do I walk?
(A) 52 m
(B) 48 m
(C) 54 m
(D) 50 m
(E) 56 m
This is Liam's timetable for a normal school day.

How many minutes of class time does Liam have every day?
(A) 300
(B) 250
(C) 500
(D) 270
(E) 240
The average of two numbers is 11 . One of the numbers is 6 more than the other. Which is the larger number?
(A) 6
(B) 8
(C) 11
(D) 14
(E) 17
What fraction of the rectangle is shaded?

(A) \(\frac{1}{3}\)
(B) \(\frac{5}{12}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{2}{7}\)
(E) \(\frac{3}{8}\)
In a group of 55 students, exactly 39 are enrolled in mathematics and exactly 35 are enrolled in science. How many students are enrolled in both mathematics and science?
(A) 20
(B) 16
(C) 19
(D) 4
(E) 55
Jeremy decides to measure area in hexagonal units (instead of squares) using the hexagonal unit as shown.
What is the area of the triangle in Jeremy's hexagonal units?

(A) 4
(B) \(4 \frac{1}{6}\)
(C) \(4 \frac{1}{3}\)
(D) \(4 \frac{1}{2}\)
(E) 3

To make a quilt 120 cm by 90 cm for my baby's cot, I add borders to a central panel as shown. If the borders are the same width all the way around, then the dimensions of the central panel, in centimetres, could be
(A) 100 by 60
(B) 90 by 60
(C) 90 by 70
(D) 86 by 36
(E) 75 by 50
Place the numbers \(1,2,3,4\) and 5 , one in each circle in the diagram so that no number is joined by a line to a consecutive number.

The sum of the numbers \(X\) and \(Y\) could be
(A) 3
(B) 4
(C) 6
(D) 7
(E) 8
Below is a diagram of a garden. Some of the garden is grass and some is a pathway made from square blocks.
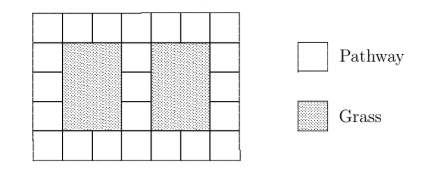
The total area of the grass is 108 square metres.
What is the area, in square metres, of the pathway?
(A) 216
(B) 54
(C) 181
(D) 207
(E) 200
A shop has a sale and sells hats for \(\$ 12\) each in the morning, taking \(\$ 720\). After lunch, the price is dropped to \(\$ 9\) each and the shop sells twice as many. What was the total amount taken on the day?
(A) \(\$ 1800\)
(B) \(\$ 900\)
(C) \(\$ 1260\)
(D) \(\$ 1440\)
(E) \(\$ 2880\)
The areas, in square centimetres, of three rectangles are given.

What is the area, in square centimetres, of the shaded rectangle?
(A) 36
(B) 48
(C) 56
(D) 60
(E) 70
Mike thinks of a two-digit number. Karen reverses the digits and when the two numbers are added the total is 132 . How many different numbers could Mike have thought of?
(A) 4
(B) 7
(C) 8
(D) 10
(E) 12
Two bolts and two screws weigh as much as one bolt and ten nails. One bolt weighs as much as one screw and one nail. How many nails weigh as much as one bolt?
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7
My birthday is 18 November. Four of my friends' birthdays are 1 November, 12 November, 21 November and 1 December. The five of us decide to hold a birthday party on the date closest to all the birthdays. (This means that the sum of the days from the chosen date to each birthday is as small as possible.) Which date should this be?
(A) 12 November
(B) 19 November
(C) 15 November
(D) 18 November
(E) 17 November
Annie is recording the number of cars in the family of each child in her class in a column graph. She has not drawn the column for the number of families that have exactly two cars.

The average number of cars per family is \(1 \frac{1}{3}\). How many families have exactly two cars?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Five rectangles, each 12 cm long and of equal width, are placed together to form a single rectangle, still 12 cm long but 5 times as wide. The new rectangle has a perimeter twice as great as each of the original rectangles. What is the perimeter, in centimetres, of the new rectangle?
(A) 48
(B) 60
(C) 64
(D) 72
(E) 84
Consider this statement:
THIS IS ONE GREAT MATHS CHALLENGE
Every minute, the first letter of each word is moved to the other end of the word. In how many minutes will the original sentence appear back again?
Below is an example of a triangle drawn on a 6 by 5 grid with one vertex \(A\) on the bottom left-hand corner and the other two vertices on the top and right-hand boundaries.
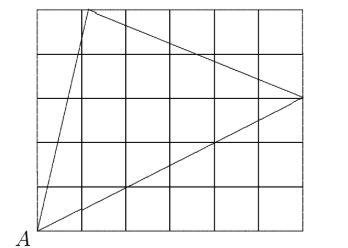
What is the largest number of squares that can be cut by the sides of such a triangle?
The product of three consecutive whole numbers is 12144 . What is their sum?
When a number has the digit 2 put at both ends, its value increases by 2785 . What is the original number?
I have 4 black and 4 white cubes of equal size. In how many different ways can they be put together to form a \(2 \times 2 \times 2\) cube? (Two cubes are not considered different if they can be rotated to look the same.)