Australian Mathematics Competition - 2009 - Upper Primary - Grade 5 & 6 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesFor the number below, what number will be obtained if I double the ten-thousands digit and halve the hundreds digit?

(A) 28824
(B) 44224
(C) 44824
(D) 14824
(E) 28224
When Sam doubled a number and then added 7, it became 33. What was the original number?
(A) 8
(B) 13
(C) 16
(D) 24
(E) 26
Which of the following is closest to 1000 seconds?
(A) 1 hour
(B) 1 day
(C) 45 minutes
(D) 30 minutes
(E) 15 minutes
The net below is folded to form a cube.
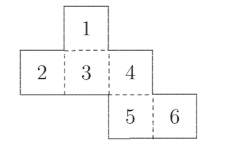
On this cube, what number is on the face opposite the number \(6 ?\)
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
What is the angle, in degrees, between the hands of a clock showing \(1: 20\) ?
(A) 40
(B) 45
(C) 80
(D) 100
(E) 120

The following shape was made from blocks that look like this
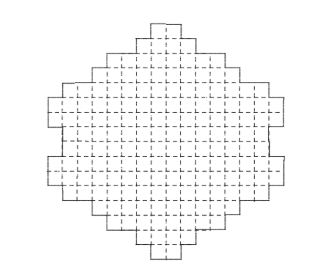
How many blocks were used to create the shape?
(A) 12
(B) 13
(C) 14
(D) 15
(E) 16
The cost for every 15 minutes in a car parking meter is 20 c. Jake put a \(\$ 1\) coin and two 20 c coins into the meter at \(1: 15 \mathrm{pm}\). At what time did the parking meter expire?
(A) \(2: 30 \mathrm{pm}\)
(B) \(3: 00 \mathrm{pm}\)
(C) \(2: 45 \mathrm{pm}\)
(D) \(3: 05 \mathrm{pm}\)
(E) \(3: 15 \mathrm{pm}\)
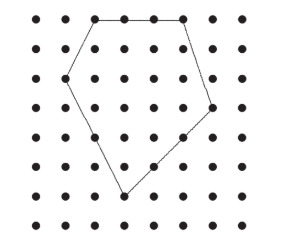
Bill walked around this path shaped like a regular pentagon. He started at the dot and walked around clockwise.

On which section of the path was he when he had gone \(65 \%\) of the way around?
(A) \(a\)
(B) \(b\)
(C) \(c\)
(D) \(d\)
(E) \(e\)
Five cars were travelling at different speeds. From the following speeds, which car was travelling the fastest?
(A) 1 km per minute
(B) 30 km in 20 minutes
(C) \(50 \mathrm{~km} / \mathrm{h}\)
(D) 20 km in \(\frac{1}{2}\) hour
(E) 12 km in 15 minutes
Some of the squares in the diagram below have been shaded.

How many more squares need to be shaded so that \(\frac{5}{9}\) of the diagram is shaded altogether?
(A) 3
(B) 5
(C) 7
(D) 8
(E) 10
What is the area, in square centimetres, of the shape marked out on the 1-cm grid below?
(A) 18.5
(B) 19
(C) 19.5
(D) 20
(E) 20.5
Ali has a bag containing 100 jelly beans. In his bag there are equal numbers of red, blue, green, yellow and brown jelly beans. If Ali closes his eyes and takes jelly beans out of the bag one by one, what is the smallest number he needs to take out to ensure he will have five of the same colour?
(A) 5
(B) 9
(C) 20
(D) 21
(E) 25
I have \(\$ 34.20\) in \(\$ 2, \$ 1,50 \mathrm{c}\), 20 c and 10 c coins and have an equal number of each coin. That number is
(A) 7
(B) 8
(C) 9
(D) 10
(E) 11

How many triangles are there in this figure?
(A) 20
(B) 32
(C) 36
(D) 40
(E) 44
The recipe for making pancakes is:
1 egg
1 cup (250 mL) milk
1 cup flour
1 teaspoon sugar
pinch of salt
This will be enough mixture to cook 12 small pancakes.
How much milk would you need to make 42 small pancakes?
(A) 3 cups
(B) \(3 \frac{1}{2}\) cups
(C) 765 mL
(D) 1050 mL
(E) \(5 \frac{1}{4}\) cups
The ages of the three children in the Jones family add up to 14 . If their ages are multiplied together, the result is 70 . What is the age of the eldest child?
(A) 5
(B) 7
(C) 8
(D) 10
(E) 14
We form a rectangle using 24 square tiles, each 1 cm by 1 cm . Which of the following, in centimetres, could not be the perimeter?
(A) 20
(B) 22
(C) 28
(D) 36
(E) 50
Each of three coloured caps covers one of three objects. The red cap is somewhere to the left of the white cap. The coin is somewhere to the left of the bean. The green cap is somewhere to the right of the shell. The bean is somewhere to the right of the green cap. Which of the following statements is correct?
(A) The bean is under the red cap.
(B) The bean is under the green cap.
(C) The shell is under the red cap.
(D) The coin is under the white cap.
(E) The shell is under the white cap.
In an Australian netball competition, these teams are tipped to win Round 1 by three experts:
Expert A: NSW, Queensland, WA, Tasmania
Expert B: SA, Victoria, Queensland, WA
Expert C: NSW, ACT, WA, Victoria
No one tipped the Northern Territory to win. Which team did Victoria play?
(A) NSW
(B) Tasmania
(C) Queensland
(D) WA
(E) Northern Territory
Marcello says to Aiden, "If you give me one of your pencils, I'll have twice as many pencils as you."
Aiden answers, "But if you give me one of yours, we'll have the same number of pencils each."
How many pencils does Aiden have?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
A basketball team has won 30 games out of 40 played. How many of the remaining 30 games must it win to have an \(80 \%\) win record for the season?
(A) 10
(B) 15
(C) 25
(D) 26
(E) 30
A horse trainer has some carrots for the horses. He gives each horse 4 carrots and has 2 carrots left over. If he wants to give each horse 6 carrots, he needs another 22 carrots. How many horses are there in his stables?
(A) 4
(B) 5
(C) 6
(D) 11
(E) 12
I bought a map of Australia, unfolded it and marked 8 places I wanted to visit.

I then refolded the map and placed it back on the table as it was. In what order are my marks stacked from top to bottom?
(A) RTYQKAWP
(B) YKRAWTPQ
(C) RTQYKAWP
(D) YKTPRAWQ
(E) YKWARTPQ
The picture below shows a triangular prism whose faces are all either triangles or squares.

It is sliced into two pieces with a straight cut through the corners labelled \(Q, L\) and \(N\). The two pieces formed are:
(A) both triangular prisms
(B) both triangular pyramids
(C) both square prisms
(D) both square pyramids
(E) one square pyramid and one triangular pyramid
Thomas and Susie each have a number of dogs, cats and fish. They each have nine pets. Thomas has three more fish than Susie but one less dog. Susie has twice as many cats as Thomas but she has the same number of fish as Thomas has dogs. How many fish does Thomas have?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
The star shown is made up of two different-sized equilateral triangles which overlap symmetrically.

If the lighter-shaded smaller triangles each have an area of 1 square unit and the darker, larger triangles each have an area of 16 square units, what is the total area, in square units, of the whole star?
A tank is \(\frac{1}{6}\) full. When 440 litres of water are added to the tank, it is then \(\frac{5}{8}\) full. How many additional litres of water are required to fill the tank?
Problem 28:
In a television quiz show, Rachel wins 250 points for a correct answer but loses 150 points for an incorrect answer. Rachel answered 15 questions and obtained 2150 points. How many questions did she get correct?

Problem 29:
\(A B C D\) is a rectangle with area 1440 square centimetres. \(X\) is halfway along \(A B, Y\) is a third of the way along \(B C, Z\) is a quarter of the way along \(C D\). In square centimetres, what is the shaded area?
Each day Merlin places the same number of flowers (at least one) at three temples. To get to any temple from another he crosses a magic river once. He also has to cross a magic river once to get to the first temple. Each time he crosses a magic river, the number of flowers he has doubles. He has no flowers left when he leaves the third temple. What is the minimum number of flowers he must have at the start?
