Australian Mathematics Competition - 2009 - Middle Primary - Grade 3 & 4 - Questions and Solutions

Problem 1:

The value of $1000+200+4$ is
(A) 10204
(B) 1204
(C) 1000204
(D) 10002004
(E) 124

Problem 2:

For the number below, what number will be obtained if I double the thousands digit and halve the tens digit?

(A) 2224
(B) 8214
(C) 4414
(D) 8244
(E) 2214

Problem 3:

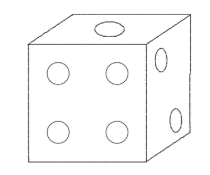
A normal dice is shown in the diagram. What is the total of the numbers on the faces not shown?
(A) 7
(B) 11
(C) 13
(D) 14
(E) 15

Problem 4:

To what number do I add 11 to get $28 ?$
(A) 39
(B) 17
(C) 27
(D) 7
(E) 19

Problem 5:

Which of the following is closest to 1000 seconds?
(A) 1 hour
(B) 1 day
(C) 45 minutes
(D) 30 minutes
(E) 15 minutes

Problem 6:

The net below is folded to form a cube.

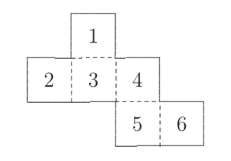
On this cube, what number is on the face opposite the number 6 ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

Problem 7:

Which of the following stories could match this number sentence?

$$
14-7+9=16
$$

(A) Simon had 14 lollies, he ate 9 of them and then his sister gave him 9 more. He then had 16 lollies.
(B) James had 18 lollies, he gave 14 to his sister, he ate 9 and had 7 left.
(C) Lan had 14 lollies, she ate 7 of them, then was given 9 more by her mother. She now has 16 lollies.
(D) Karen ate 14 lollies, took 7 from her sister, ate 9 more and had 16 left.
(E) Helen had 14 lollies, was given 7 more by her brother and 9 more by her sister and now has 16 lollies.

Problem 8:

Some friends are playing darts. Their darts land at the points $(6,7),(2,3),(7,6),(3,5)$ and $(1,6)$. Which dart scored the highest?
(A) the dart at $(6,7)$
(B) the dart at $(2,3)$
(C) the dart at $(7,6)$
(D) the dart at $(3,5)$
(E) the dart at $(1,6)$

Problem 9:

A string of beads has a repeating pattern of blue, red, red, green, yellow and yellow. Starting from green, what is the colour of the 18th bead?
(A) red
(B) green
(C) blue
(D) yellow
(E) orange

Problem 10:

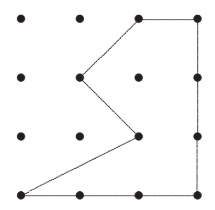
The grid is a 1-centimetre grid. What is the area, in square centimetres, of the figure shown?
(A) $3 \frac{1}{2}$
(B) 4
(C) $4 \frac{1}{2}$
(D) 5
(E) $5 \frac{1}{2}$

Problem 11:

I read 3 chapters of my book each night except Saturday and Sunday when I read 4 chapters each night. How many chapters do I read in a week?
(A) 8
(B) 15
(C) 21
(D) 23
(E) 29

Problem 12:

Given the roads and distances marked below, how far is it by road, in kilometres, from Cobra to Kairo?

(A) 30
(B) 45
(C) 60
(D) 71
(E) 80

Problem 13:

When a barrel is one-quarter full it contains 6 litres. How many litres does it hold when it is two-thirds full?
(A) 16
(B) 18
(C) 20
(D) 21
(E) 24

Problem 14:

Jye takes four steps to walk the same distance that Fred covers in three steps. If each of Fred's steps is 50 cm , what distance, in metres, does Jye walk if he takes 24 steps?
(A) 3
(B) 6
(C) 9
(D) 12
(E) 16

Problem 15:

Using $5 \mathrm{c}, 10 \mathrm{c}, 20 \mathrm{c}$ and 50 c coins, in how many different ways can you make up 50c?

(A) 4
(B) 6
(C) 8
(D) 10
(E) 13

Problem 16:

Five teams play each other once in a basketball competition. How many games were played in total?
(A) 10
(B) 12
(C) 14
(D) 20
(E) 28

Problem 17:

How many triangles are there in this figure?
(A) 20
(B) 32
(C) 36
(D) 40
(E) 44

Problem 18:

The recipe for making pancakes is:
1 egg
1 cup ( 250 mL ) milk
1 cup flour
1 teaspoon sugar
pinch of salt
This will be enough mixture to cook 12 small pancakes.
How much milk would you need to make 42 small pancakes?
(A) 3 cups
(B) $3 \frac{1}{2}$ cups
(C) 765 mL
(D) 1050 mL
(E) $5 \frac{1}{4}$ cups

Problem 19:

The picture shows a cube with some corners labelled. It is cut into two pieces by making a straight cut from $P Q$ to $R S$. The two pieces formed are:
(A) both triangular prisms
(B) both triangular pyramids
(C) both square prisms
(D) both square pyramids
(E) one square pyramid and one triangular pyramid

Problem 20:

I live in a small street with 6 houses. One day 35 letters were delivered in my street and I received more letters than anyone else. What is the smallest number of letters I could have received?
(A) 1
(B) 3
(C) 5
(D) 7
(E) 8

Problem 21:

The ages of the three children in the Jones family add up to 14 . If their ages are multiplied together, the result is 70 . What is the age of the eldest child?
(A) 5
(B) 7
(C) 8
(D) 10
(E) 14

Problem 22:

We form a rectangle using 24 square tiles, each 1 cm by 1 cm . Which of the following, in centimetres, could not be the perimeter?
(A) 20
(B) 22
(C) 28
(D) 36
(E) 50

Problem 23:

I bought a map of Australia, unfolded it and marked 8 places I wanted to visit.

I then refolded the map and placed it back on the table as it was. In what order are my marks stacked from top to bottom?
(A) RTYQKAWP
(B) YKRAWTPQ
(C) RTQYKAWP
(D) YKTPRAWQ
(E) YKWARTPQ

Problem 24:

Jeremy replaces one digit by the symbol $\triangle$ and another by the symbol $\triangle$. Given that the sum

is correct, which digit does the symbol $\triangle$ represent?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6

Problem 25:

Our family's cat and dog together weigh 7 kg . Our dog and rabbit together weigh 6 kg . Our cat and rabbit together weigh 5 kg .

In kilograms, how much does our cat weigh?
(A) 2
(B) 2.5
(C) 3
(D) 3.5
(E) 4

Problem 26:

Sally has a pile of jelly beans. Her brother eats half of them, then her sister eats a quarter of the remaining jelly beans. Her father finds the leftover jelly beans and eats one-third of them leaving Sally with 6 jelly beans. How many jelly beans did Sally have to begin with?

Problem 27:

Ms Davey has a box of marbles in her storeroom. She can share her marbles equally between $2,3,4,5$ or 6 children with no marbles leftover. What is the smallest number of marbles that could be in Ms Davey's box?

Problem 28:

In the diagram, 6 equal polygons touch as shown, and each of them contains a number from 1 to 6 .

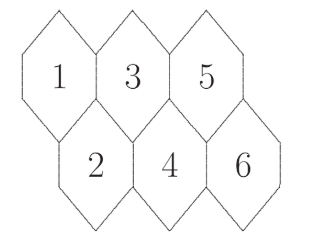
How many ways are there to move from polygon 1 to polygon 6 if you can move only to a touching polygon labelled with a larger number?

Problem 29:

In a television quiz show, Rachel wins 250 points for a correct answer but loses 150 points for an incorrect answer. Rachel answered 15 questions and obtained 2150 points. How many questions did she get correct?

Problem 30:

Each day Merlin places the same number of flowers (at least one) at three temples. To get to any temple from another he crosses a magic river once. He also has to cross a magic river once to get to the first temple. Each time he crosses a magic river, the number of flowers he has doubles. He has no flowers left when he leaves the third temple. What is the minimum number of flowers he must have at the start?