Australian Mathematics Competition - 2008 - Upper Primary - Grade 5 & 6 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesWhat is the largest 4 -digit number which can be made from a selection of the following number cards if each card may be used only once?

(A) 4581
(B) 8542
(C) 8541
(D) 5480
(E) 8851
What is the number represented on the number line?

(A) 0.3
(B) 3
(C) 13
(D) 1.03
(E) 1.3
If 100 tickets are sold in a class raffle, how many tickets will Matthew have to buy to have a \(\frac{1}{10}\) chance of winning?
(A) 100
(B) 1
(C) 20
(D) 10
(E) 5
A water tank holds 7500 litres when full. How many litres does it hold when it is exactly half full?
(A) 3275
(B) 3500
(C) 4000
(D) 3750
(E) 3725
If 1 bottle of water can fill 3 glasses, how many glasses of the same size would be filled with 7 bottles of water?
(A) 21
(B) 24
(C) 14
(D) 18
(E) 25
The cost of petrol is 149.9 cents per litre on a Tuesday and 153.5 cents per litre the next morning. What was the increase in cents per litre overnight?
(A) 6.4
(B) 4.3
(C) 16.4
(D) 3.5
(E) 3.6
Jill walked along a two-kilometre track. How far had she walked if she had walked \(\frac{3}{4}\) of the track?
(A) \(1 \frac{1}{2} \mathrm{~km}\)
(B) 175 metres
(C) 300 metres
(D) 1750 metres
(E) 1.34 km
Which of the following shapes could not be formed from a number of equal-sized equilateral triangles?
(A) rhombus
(B) trapezium
(C) square
(D) hexagon
(E) parallelogram
Jenny has three boxes, each having the same number of toy cars inside. She finds two more cars down the back of the sofa. When she counts all her cars she finds that she has 17 . How many cars are there in each box?
(A) 3
(B) 5
(C) 6
(D) 8
(E) 15
In the number sentence,\[40 \times 40=20 \times 20 \times \square \]
what number do we put in the \(\square\) to make the number sentence true?
(A) 2
(B) 4
(C) 8
(D) 16
(E) 40
A box holds socks which are all the same size. There are 6 white, 10 blue and 16 grey socks. What is the least number of socks I need to take out, without looking, so that I can be certain of getting a pair of matching socks?
(A) 3
(B) 4
(C) 5
(D) 6
(E) 10
Kiesha has a fish tank which is the right size for 3 fish. A friend gave her 3 more fish and she needs to get a tank with double the volume. She could do this by buying a new tank which is:
(A) double the width and the length of the old tank
(B) double the width, length and depth of the old tank
(C) half the length and double the width and depth of the old tank
(D) half the length and double the depth of the old tank
(E) half the length and double the width of the old tank
If Joachim has 26 m of garden fencing, how many different ways can he make a rectangular garden, using all the fencing, if each side of his garden is a whole number of metres?
(A) 8
(B) 6
(C) 4
(D) 2
(E) 1
At half-time in a soccer match between Newcastle and Melbourne, the score was Newcastle 1, Melbourne 0 . Three goals were scored in the second half. Which of the following could not be the result of the match?

(A) The match was drawn
(B) Newcastle won by 2 goals
(C) Melbourne won by 2 goals
(D) Newcastle won by 1 goal
(E) Newcastle won by 4 goals
Two 1 litre jugs are each filled with a mixture of olive oil and vinegar. The first jug has three times as much oil as vinegar and the second has four times as much oil as vinegar. They are poured into a larger container. In the new mixture, the volume of oil will be
(A) 750 mL
(B) 800 mL
(C) 1250 mL
(D) 1450 mL
(E) 1550 mL
In a circle dance, everyone is evenly spaced around a circle and has a number in the order \(1,2,3,4,5, \ldots\), and so on. The dancer with number 15 is directly opposite dancer number 3 . How many dancers are in the circle?
(A) 18
(B) 20
(C) 22
(D) 24
(E) 26
In the \(5 \times 5\) square below, the numbers \(1,2,3,4\) and 5 are to be placed in the squares so that each number appears exactly once in each row and once in each column. Some numbers have already been placed.

When the square is completed, the number which is in the square marked with an X is
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
The perimeter of this rectangular paddock is 700 m . It is subdivided into six identical paddocks as shown.
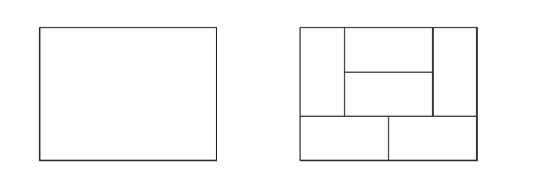
The perimeter, in metres, of each of the six smaller paddocks is
(A) \(116 \frac{1}{3}\)
(B) 300
(C) 200
(D) 150
(E) 600
You roll three regular 6-sided dice. The product of the numbers rolled is 24 . What is the maximum possible sum of three such numbers?
(A) 8
(B) 9
(C) 10
(D) 11
(E) 12
Which of the following methods would divide seven identical loaves of bread equally between 12 hungry people?
(A) cut 5 into quarters and 2 into thirds
(B) cut 3 into thirds and 4 into quarters
(C) cut 5 into thirds and 2 into quarters
(D) cut 3 into quarters and 4 into thirds
(E) cut 5 into halves and 2 into thirds
Three water pipes can be used to fill a water tank. The first pipe by itself takes 8 hours to fill the tank, the second pipe by itself takes 12 hours to fill the tank and the third pipe by itself takes 24 hours to fill the tank. How long would it take to fill the tank from empty if all pipes were used at the same time?
(A) 2 hrs
(B) 3 hrs
(C) 6 hrs
(D) 5 hrs
(E) 4 hrs
The average age of the 11 players in the Australian soccer team is 22.

One player got a red card and had to leave the field. Then, the average age of the remaining 10 players on the field was 21 . How old was the player with the red card?
(A) 21
(B) 31
(C) 22
(D) 32
(E) 24
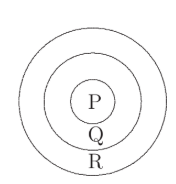
Anne designs the dart board shown, where she scores \(P\) points in the centre circle, \(Q\) points in the next ring and \(R\) points in the outer ring. She throws three darts in each turn. In her first turn, she gets two darts in ring \(Q\) and one in ring \(R\) and scores 10 points. In her second turn, she gets two in circle \(P\) and one in ring \(R\) and scores 22 points.
In her next turn, she gets one dart in each of the regions. How many points does she score?
(A) 12
(B) 13
(C) 15
(D) 16
(E) 18
Paradise is a circular island. There are 4 villages on the island at the \(\mathrm{N}, \mathrm{E}, \mathrm{S}\) and SE points. Each village has fishing rights for a single continuous strip of coastline, which must include the village plus 3 km either side. If the fishing rights are distributed as evenly as possible between the four villages under the above rules, and the difference between the length of coastline fished by the village at N and the village at SE is as small as possible, then this difference, in kilometres, is
(A) 6
(B) 9
(C) 12
(D) 15
(E) 36
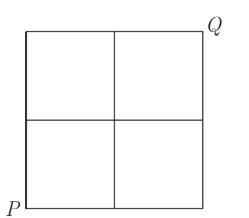
A town centre has a series of roads which form a two by two square as shown. On any particular journey from \(P\) to \(Q\), I may not drive down the same section of road twice, though I may cross any intersection more than once. How many different journeys are there from \(P\) to \(Q\) ?
(A) 6
(B) 10
(C) 12
(D) 14
(E) 16
What is the largest number less than 1000 , which is odd, leaves a remainder of 2 when divided by 3 , and a remainder of 4 when divided by \(5 ?\)
A cube with edge length 1 m is cut up into cubes each with edge length 5 cm . If all these cubes were stacked one on top of the other to form a tower, what would be the height, in metres, of this tower?
A beetle sets out on a journey. On the first day it crawls 1 m in a straight line. On the second day it makes a right-angled turn (in either direction) and crawls 2 m in a straight line. On the third day it makes a right-angled turn (in either direction) and crawls 3 m in a straight line. This continues each day with the bug making a rightangled turn (in either direction) and crawling 1 m further than it did the day before. What is the least number of days before the beetle could find itself stopped at its starting point?
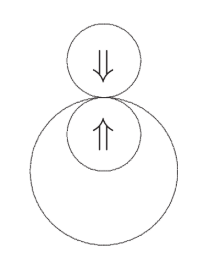
Two identical coins are placed one inside and one outside a thin circular wire, which has twice the diameter of each coin. Each coin is rolled, without slipping, around the wire until it returns to its starting point. If the direction of rotation does not matter, what is the difference, in degrees, between the angle through which the outer coin rotates and the angle through which the inner coin rotates?
I have a number of bricks which are each 3 units long, 1 unit deep and 1 unit wide. I want to stack them in a tower 3 units wide, 1 unit deep and 10 units high. In how many ways can I do this? (One such way is shown.)
