AMC 8, 2014 - Problem 14: Area of Trapezium

AMC 8, 2014 - Problem 14

A quadrilateral with at least one pair of parallel sides is called a trapezium. Area of a trapezium is half of the product of sum of the parallel sides and height. Let's find its area as the sum of the area of a rectangle and a triangle.

Try the problem

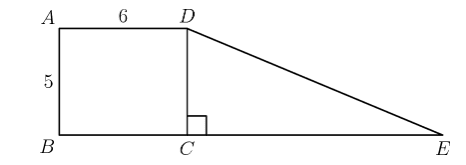
Rectangle (ABCD) and right triangle (\triangle DCE) have the same area. They are joined to form a trapezoid, as shown. What is (DE)?

((A)12\qquad(B)13\qquad(C)14\qquad(D)15\qquad(E)16)

American Mathematical Contest 2014, AMC 8 Problem 14

Area of Trapezium

3 out of 10

Challenges and Thrills in Pre College Mathematics

Excursion Of Mathematics

Knowledge Graph

Use some hints

Area of the triangle (\triangle DCE) = \frac{DC.CE}{2}

And the area of the square = (AB.AD)

It is given that (AB=5)

Then clearly (AB=DC=5)

(\frac{5.CE}{2}=30) , (30 is the area of the square)

This gives the value of (CE)

Now applying Pythagorean theorem in (\triangle ACE)

(DE^{2}=CE^{2}+DC^{2})

Which gives (DE=13)

AMC 8, 2014 - Problem 14: Area of Trapezium