Area of Region in a Circle | AMC-10A, 2011 | Problem 18

Try this beautiful problem from Geometry based on Area of Region in a Circle.

Area of Region in a Circle - AMC-10A, 2011- Problem 18

Circles $A, B,$ and $C$ each have radius 1. Circles $A$ and $B$ share one point of tangency. Circle $C$ has a point of tangency with the midpoint of $\overline{AB}$. What is the area inside Circle $C$ but outside circle $A$ and circle $B$ ?

$\pi$
$\frac{3\pi}{2}$
$2$
$6$
$\frac{5\pi}{2}$

Key Concepts

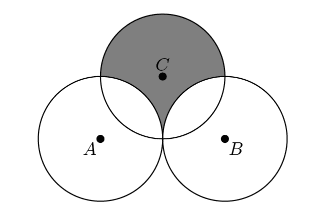
Geometry

Circle

Rectangle

Check the Answer

Answer: $2$

AMC-10A (2011) Problem 18

Pre College Mathematics

Try with Hints

We have to find out the area of the shaded region .Given that three circles with radius $1$ and Circle $C$ has a point of tangency with the midpoint of $\overline{AB}$.so if we draw a rectangle as shown in given below then we can find out the required region by the area of half of $C$ plus the area of the rectangle minus the area of the two sectors created by $A$ and $B$

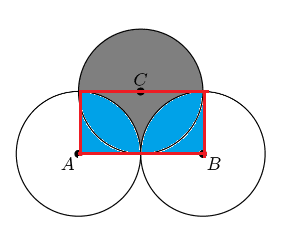
can you finish the problem........

Now area of the rectangle is $2\times 1=2$

Area of the half circle with center (gray shaded region)=$\frac{\pi (1)^2}{2}$

The area of the two sectors created by $A$ and $B$(blue region)=$\frac{2\pi(1)^2}{4}$

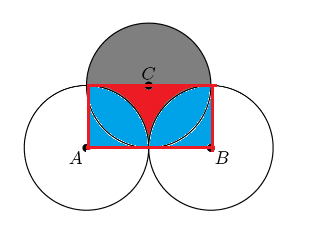
can you finish the problem........

Therefore, the required region (gray region)=area of half of $C$ plus the area of the rectangle minus the area of the two sectors created by $A$ and $B$=$\frac{\pi (1)^2}{2}$+$2\times 1=2$-$\frac{2\pi(1)^2}{4}$=$2$

Area of Region in a Circle | AMC-10A, 2011 | Problem 18