Australian Mathematics Competition - 2023 - Intermediate - Grade 9 & 10 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesA 40-minute lesson started at 10:50 am. Exactly halfway through the lesson the fire alarm went off. At what time did the fire alarm go off?
(A) 10:30 am
(B) 11:00 am
(C) 11:10 am
(D) \(11: 20 \mathrm{am}\)
(E) 11:30 am

Two rectangles have a vertex in common, as shown. What is the size of the angle marked \(x^{\circ}\) between them?
(A) \(10^{\circ}\)
(B) \(20^{\circ}\)
(C) \(30^{\circ}\)
(D) \(40^{\circ}\)
(E) \(50^{\circ}\)
What is the value of \(\frac{2+3+4}{7+8+9}\) ?
(A) \(\frac{1}{6}\)
(B) \(\frac{2}{7}\)
(C) \(\frac{3}{8}\)
(D) \(\frac{4}{9}\)
(E) \(\frac{1}{2}\)

How many \(25 \mathrm{~cm} \times 25 \mathrm{~cm}\) squares fit in a \(50 \mathrm{~cm} \times 1 \mathrm{~m}\) rectangle?
(A) 1
(B) 2
(C) 4
(D) 6
(E) 8
Which one of these is equal to \(57 \times 953\) ?
(A) 321
(B) 4321
(C) 54321
(D) 654321
(E) 7654321
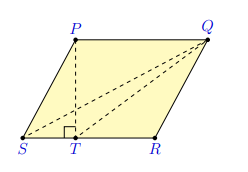
A parallelogram (P Q R S) has an area of \(60 \mathrm{~cm}^2\) and side (P Q) of length 10 cm .
Which length is 6 cm ?
(A) \(R Q\)
(B) \(R S\)
(C) \(Q T\)
(D) \(P T\)
(E) \(Q S\)
Mei can travel to her grandma's house by a direct route, or by a scenic route that is 5 km longer. When she travels by the scenic route, and comes directly home, the round trip is 35 km . How long is the direct route?
(A) 5 km
(B) 12.5 km
(C) 15 km
(D) 20 km
(E) 22.5 km
What is the value of \(\left(\left(2^0\right)^2\right)^3\) ?
(A) 1
(B) 12
(C) 32
(D) 64
(E) 256
What must 0.05 be divided by to get 50 ?
(A) 1000
(B) 100
(C) 0.1
(D) 0.001
(E) 0.0001

In the right-angled triangle (A B C) shown, what is the value of (y) ?
(A) 45
(B) 48
(C) 54
(D) 60
(E) 72
The number 11 can be written as the sum of three positive whole numbers in many ways. In how many ways can this be done where the numbers are different and in increasing order?
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7
A two-digit number is reversed then added to itself. The answer cannot be
(A) 55
(B) 110
(C) 132
(D) 154
(E) 186

Amy designed this rectangular flag for her fleet of yachts. What fraction of the flag is shaded?
(A) \(\frac{2}{3}\)
(B) \(\frac{3}{5}\)
(C) \(\frac{5}{8}\)
(D) \(\frac{1}{2}\)
(E) \(\frac{7}{12}\)
What is the largest possible whole-number value of the expression \(a \times b+\frac{c}{d}-\frac{e}{f}\) where \(a, b, c, d, e, f\) are the numbers \(1,2,3,4,5\) and 6 in some order?
(A) 30
(B) 31
(C) 32
(D) 33
(E) 34
Four children named, from youngest to oldest, Abdul, Bipin, Cai and Denise have ages which are equally spaced apart. Abdul and Bipin's ages add to 18, whilst Cai and Denise's ages add to 34 . How old is Denise?
(A) 14
(B) 16
(C) 18
(D) 19
(E) 20
The country of Exponentia uses six-digit telephone numbers. At the moment, this is plenty, since there are only 1000 phone numbers in use. However, increasing population and phone usage means that the number of phone numbers needs to double each year. Approximately how many years will it take for Exponentia to run out of phone numbers?
(A) 5
(B) 10
(C) 20
(D) 30
(E) 40

A \(15 \mathrm{~cm} \times 15 \mathrm{~cm}\) square of origami paper is dark blue on top and pale yellow underneath. The top-left corner is folded down so that a crease is made from the top-right corner to a point \(x \mathrm{~cm}\) above the bottom-left corner. Once folded, the visible regions of yellow and blue paper have equal areas. What is the value of \(x\) ?
(A) 5
(B) \(6 \frac{2}{3}\)
(C) \(3 \sqrt{3}\)
(D) 6
(E) \(4 \sqrt{2}\)
In this equation, the coefficient of \(y\) has been hidden, but we know that it is a positive integer, 1 or more.

The equation has at least one solution where \(x\) and \(y\) are positive integers. How many different values are possible for the hidden coefficient?
(A) 10
(B) 12
(C) 13
(D) 24
(E) 25
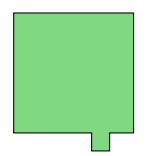
Farmer Smith had a square property that he extended by buying a smaller square of land, creating the property shown. The new square of land increased the total perimeter of the property by \(10 \%\).
By what percentage did the area of the property increase?
(A) 2
(B) 4
(C) 6
(D) 8
(E) 10
I hear that dogs age 7 dog years every year. My dog Ruby was born on my ninth birthday. Four years from now, on our birthday, Ruby's age in dog years will be exactly four times my age in normal years. How old am I now?
(A) 10
(B) 12
(C) 13
(D) 15
(E) 17
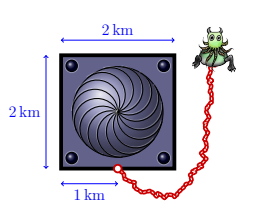
An ancient beast guards a \(2 \mathrm{~km} \times 2 \mathrm{~km}\) square building on an otherwise featureless plain. A 4 km -long unbreakable chain connects the beast to the outside wall of the building, as shown in the diagram. Neither the beast nor the chain can cross into the area occupied by the building. What is the area that the beast can access, in square kilometres?
(A) \(9 \pi\)
(B) \(10 \pi\)
(C) \(11 \pi\)
(D) \(12 \pi\)
(E) \(13 \pi\)
I have four numbers. When I add 3 to the first number, subtract 3 from the second number, multiply the third number by 3 and divide the fourth number by 3 , my four answers are all equal. My original 4 numbers added to 32 . What is the sum of the largest two of these?
(A) 24
(B) 25
(C) 26
(D) 27
(E) 28
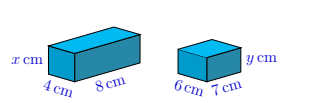
These two rectangular prisms have the same surface area. Both \(x\) and \(y\) are integers less than 10 . What is \(x+y\) ?
(A) 5
(B) 7
(C) 11
(D) 12
(E) 13
Sometimes a three-digit number is an exact multiple of its digit sum. For instance, the digit sum of 102 is \(1+0+2=3\) and \(102=3 \times 34\). If a three-digit number is \(k\) times the sum of its digits, what is the smallest possible integer value of (k) ?
(A) 9
(B) 10
(C) 11
(D) 12
(E) 13
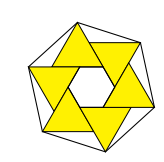
Six identical equilateral triangles of side length 2 are drawn outside a regular hexagon of side length 1 , defining a larger hexagon as shown. What is the ratio of the area of the larger hexagon to the area of the smaller hexagon?
(A) \(5: 1\)
(B) \(6: 1\)
(C) \(7: 1\)
(D)\(8: 1\)
(E) \(9: 1\)
Seána was arranging her collection of postage stamps into groups when a cat jumped onto them and scattered the stamps. All she can remember is that when she put them into groups of \(2,3,4,5\) or 6 she always had 1 stamp left over. When she placed them into groups of 7 there were none left over. What is the minimum number of stamps Seána could have had in her collection?

A square \(A B C D\) is inscribed in a right-angled triangle \(E F G\) as shown.
The length of \(E G\) is 4 units and the length of \(E F\) is 3 units. As a fraction in simplest form, the side-length of the square is \(\frac{a}{b}\). What is the value of \(a+b\) ?
The elves have to choose who will go the annual magic conference. They sit in a circle and the chief elf Elvin starts counting round the circle, starting with himself. Every second elf counted drops out of the circle and the counting continues until Elvin drops out. All those left in the circle go to the conference. This year, there are 1000 elves in the circle. How many will go to the conference?

Two wheels are fixed to an axle as shown. Due to their different sizes, the two wheels trace two concentric circles when rolled on level ground. In centimetres, what is the radius of the circle traced on the ground by the larger wheel?
A tromino is a shape made from three squares traced on gridlines. A \(2 \times 3\) grid can be tiled by trominoes in exactly three ways, as shown.

We count two tilings that are reflections of each other as different. Similarly, two tilings that are rotations of each other are counted as different. In how many different ways can a \(3 \times 6\) grid be tiled by trominoes?