Solution: Australian Mathematics Competition 2022 – Upper Primary, Problem 16
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free Resources
Let's discuss a problem from AMC 2022 - Upper Primary - 16 on Geometry.
Three different squares are arranged as shown. The perimeter of the largest square is $32$ centimetres. The area of the smallest square is $9$ square centimetres. What is the perimeter of the medium-sized square? (AMC 2022 - Upper Primary - 16)
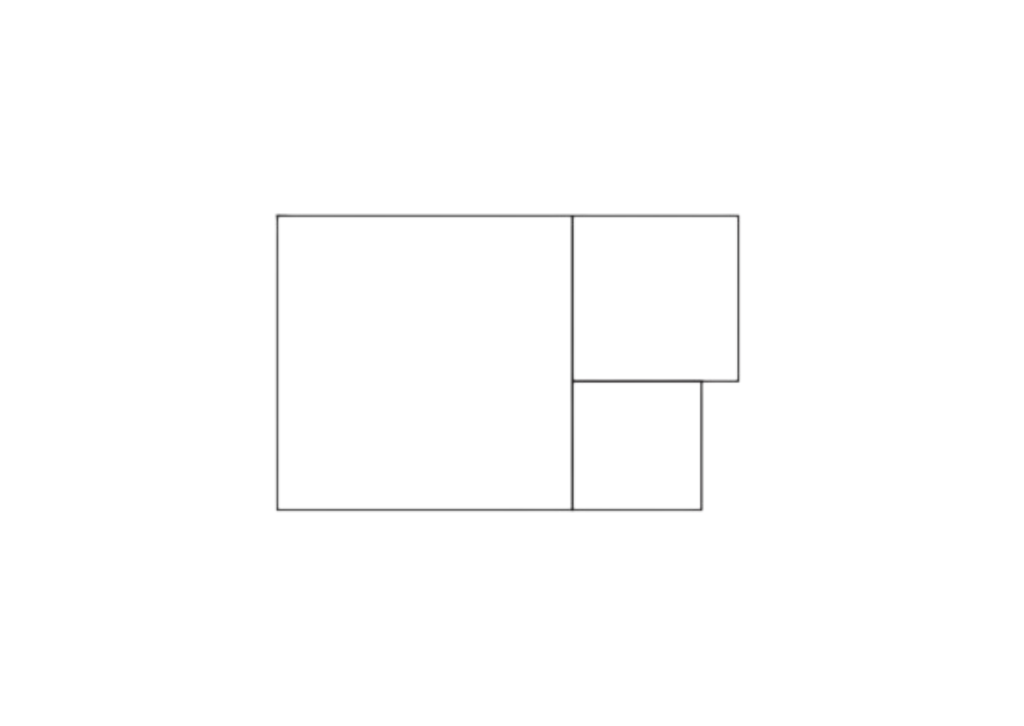
(A) 12 cm (B) 14 cm (C) 20 cm (D) 24 cm (E) 30 cm
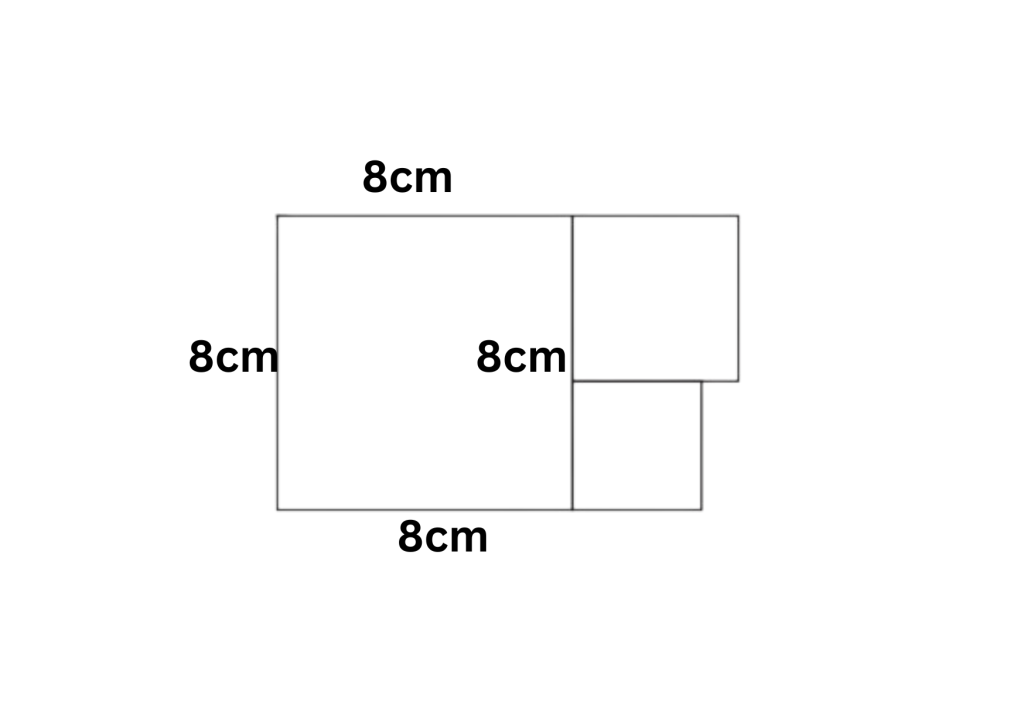
In this problem, it is given that the big square has a perimeter of \(32\)cms. We know how to find the perimeter of a square.
The perimeter is nothing but the length of the boundary. So \(4a\) is the perimeter of a square. Thus \(4a = 32\),
so, \(a = \frac {32}{4} = 8\).
Thus the side length of the bigger square is = \(8\)cms.
The small square has the area as \(9\) sq cms.
The area of a square is = \( a^2\). Thus \(a^2 = 9, a = 3\).
Thus the side length of the smallest square is 3 cms.
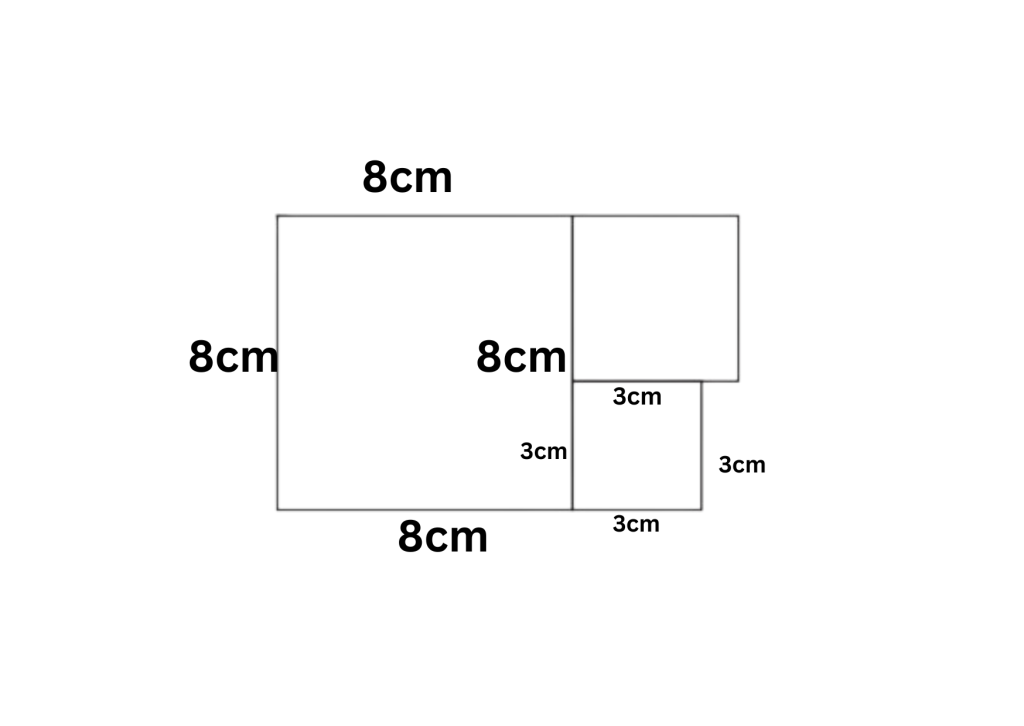
Thus the medium square has a side length of = \(8-3\) cm = \(5\)cm.
Thus the perimeter of the medium square is = \(4a = 4 \times 5 = 20\) cm.
The Australian Mathematics Competition (AMC) is one of the largest and oldest annual mathematics competitions in Australia, aimed at fostering interest and excellence in mathematics among students