Australian Mathematics Competition - 2022 - Intermediate - Grade 9 & 10 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free Resources\(2220-2022=\)
(A) 18
(B) 188
(C) 198
(D) 200
(E) 202

This shape is built from 29 squares, each \(1 \mathrm{~cm} \times 1 \mathrm{~cm}\). What is its perimeter in centimetres?
(A) 52
(B) 58
(C) 60
(D) 68
(E) 72

A digital clock shows the time as 20:22.
In how many minutes will it be midnight?
(A) 158
(B) 218
(C) 258
(D) 278
(E) 378
The value of \(\frac{1^2+2^2}{3^2+4^2}\) is
(A) \(\frac{1}{5}\)
(B) \(\frac{3}{7}\)
(C) \(\frac{9}{49}\)
(D) 4
(E) 5

In the triangle \(P Q R\) shown, \(P Q=P R\) and \(\angle Q P R=48^{\circ}\). What is \(\angle P Q R\) ?
(A) \(60^{\circ}\)
(B) \(66^{\circ}\)
(C) \(72^{\circ}\)
(D) \(78^{\circ}\)
(E) \(84^{\circ}\)

What fraction of this rectangle is shaded?
(A) \(\frac{1}{2}\)
(B) \(\frac{5}{8}\)
(C) \(\frac{5}{6}\)
(D) \(\frac{2}{3}\)
(E) \(\frac{7}{12}\)
\((0.4)^2+(0.1)^2=\)
(A) 0.25
(B) 1.7
(C) 0.17
(D) 1
(E) 0.26
Australia uses 160 million litres of petrol each day.
There is enough petrol stored to last 60 days.
How much more petrol does Australia need to buy to have enough stored for 90 days?
(A) 4 million litres
(B) 4.8 million litres
(C) 480 million litres
(D) 160 million litres
(E) 4800 million litres
\(\frac{2022}{2}-\frac{2022}{3}=\)
(A) 337
(B) 674
(C) 2022
(D) -2022
(E) -674
Which algebraic term should replace \(\triangle\) in the equation below?
\[\triangle+\triangle+\triangle=27 x^3 y^6\]
(A) \(3 x y^2\)
(B) \(3 x^3 y^6\)
(C) \(9 x y^2\)
(D) \(9 x^3 y^6\)
(E) \(27 x y^2\)

Three vertices of a rectangle are the points \((1,4)\), \((7,4)\) and \((1,8)\). At which point do the diagonals of the rectangle cross?
(A) \((4,6)\)
(B) \((3,2)\)
(C) \((3,1)\)
(D) \((5,6)\)
(E) \((7,8)\)
What value should be placed in the box to satisfy the equation?

(A) 1
(B) \(1 \frac{1}{2}\)
(C) 2
(D) \(2 \frac{1}{2}\)
(E) 3
The angles of a triangle are in the ratio \(2: 3: 4\). What is the size of the largest angle in degrees?
(A) 40
(B) 45
(C) 72
(D) 80
(E) 90
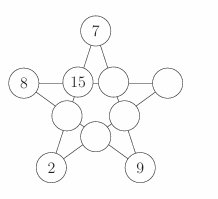
In this puzzle, each circle should contain an integer. Each of the five lines of four circles should add to 40 . When the puzzle is completed, what is the largest number used?
(A) 15
(B) 16
(C) 17
(D) 18
(E) 19
Daniel and Luke arrange to meet at a cafe. Luke leaves work, walking at \(6 \mathrm{~km} / \mathrm{h}\). Five minutes later, Daniel starts cycling from his flat at \(20 \mathrm{~km} / \mathrm{h}\). A further 15 minutes later, both arrive at the cafe at the same time.
What is the total distance they travelled?
(A) 5.5 km
(B) 6 km
(C) 6.5 km
(D) 7 km
(E) 7.5 km
My family of 7 adults and 5 children gather each year to celebrate Chinese MidAutumn festival. Each adult gives one gift to everyone else. Each child gives one gift to every other child. How many gifts are given?
(A) 78
(B) 85
(C) 97
(D) 102
(E) 109

This spinner is spun twice to form a two-digit number using the following rules:
What is the probability that the resulting two-digit number is divisible by 11 ?\(A\) \(\frac{1}{4}\)
(B) \(\frac{3}{8}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{5}{8}\)
(E) \(\frac{9}{16}\)

Eight overlapping unit squares are drawn to produce a flower shape as shown. The parts where two squares overlap are isosceles triangles.
What is the total shaded area?
(A) 5
(B) \(5 \frac{1}{2}\)
(C) 6
(D) \(6 \frac{1}{2}\)
(E) 7
Rick and Nic started learning guitar recently.
Two weeks ago, Rick had been learning five times as long as Nic.
Two days ago, Rick had been learning twice as long as Nic.
Today, what is the number of days that Rick has been learning plus the number of days that Nic has been learning?
(A) 25
(B) 37
(C) 46
(D) 52
(E) 68
Over the last 20 years, the standard ratio of television screens has changed from (4: 3) to (16: 9). When the ratio of content doesn't match the ratio of the screen it is being viewed on, black bars are often used to compensate, as illustrated.

If \(\ell\) is the fraction of the screen blacked out in the left diagram, and \(r\) is the fraction of the screen blacked out in the right diagram, then the ratio \(\ell: r\) equals
(A) \(3: 4\)
(B) \(8: 9\)
(C) \(1: 1\)
(D) \(9: 8\)
(E) \(4: 3\)
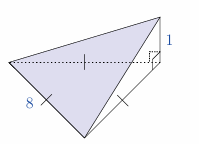
A triangular ramp is in the shape of a right-angled tetrahedron. The horizontal base is an equilateral triangle with sides 8 metres. The apex is 1 metre directly above one corner of the base, so that two faces are vertical. In square metres, what is the area of the sloping face?
(A) \(16 \sqrt{3}\)
(B) 28
(C) \(\frac{65}{4} \sqrt{3}\)
(D) \(4 \sqrt{33}\)
(E) 32
What is the value of the following expression when \(n=2022\) ?
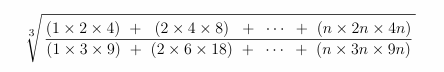
(A) \(\frac{1}{2}\)
(B) \(\frac{2}{3}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{4}{5}\)
(E) \(\frac{5}{6}\)
Lisa has a mixture of water and milk in a drum in the ratio \(5: 7\). She accidentally spills 9 L of this mixture.
She then fills the drum with 9 L of water. This makes the water to milk ratio \(9: 7\). How many litres of milk were in the drum originally?
(A) 20
(B) 21
(C) 24
(D) 36
(E) 40
Given that the highest common factor of \(p\) and \(q\) is \(t\), and \(q=r t\), then the lowest common multiple of \(p\) and \(q\) will always be equal to
(A) \(p q\)
(B) \(q r\)
(C) \(r t\)
(D) \(p r\)
(E) \(p t\)

A positive number is written in each cell of the \(3 \times 3\) table. In each row and in each column, the product of the numbers is equal to 1 . In each \(2 \times 2\) square, the product of the numbers is equal to 2 . What is the number in the central cell?
(A) 1
(B) 2
(C) 6
(D) 8
(E) 16
In the sum below, \(a, b\) and \(c\) are nonzero digits.

What is the three-digit number (a b c) in the second line of the sum?
When these numbers are multiplied, what is the sum of all digits in the answer?

In how many ways can 100 be written as the sum of three different positive integers? Note that we do not consider sums formed by reordering the terms to be different, so that \(34+5+61\) and \(61+34+5\) are treated as the same sum.
What is the largest number of distinct elements that you can choose from the set \({1,2,3,4, \ldots, 1000}\) such that no three of them are the side lengths of a triangle? For example the selection could include 20, 22 and 42 , since there is no triangle with sides 20,22 and 42 .
Problem 30:
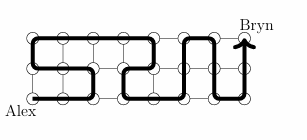
Students sit at their desks in three rows of eight. Felix, the class pet, must be passed to each student exactly once, starting with Alex in one corner and finishing with Bryn in the opposite corner. Each student can pass only to the immediate neighbour left, right, in front or behind. One possible path is shown.
How many different paths can Felix take from Alex to Bryn?