Australian Mathematics Competition - 2021 - Intermediate - Grade 9 & 10 - Questions and Solutions

Problem 1:

Each edge of this star is 2 cm long.
What is its perimeter?
(A) 5 cm
(B) 10 cm
(C) 15 cm
(D) 20 cm
(E) 25 cm

Problem 2:

The value of \(2000-200+20-2\) is
(A) 1778
(B) 1782
(C) 1818
(D) 1822
(E) 1888

Problem 3:

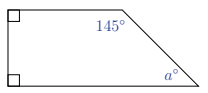
What is the value of \(a\) in the diagram?
(A) 35
(B) 45
(C) 55
(D) 65
(E) 75

Problem 4:

What is \(50 \%\) more than \(\frac{1}{2}\) ?
(A) \(\frac{1}{4}\)
(B) \(\frac{5}{8}\)
(C) \(\frac{3}{2}\)
(D) \(\frac{3}{4}\)
(E) 50.5

Problem 5:

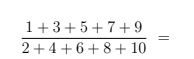
(A) \(\frac{1}{2}\)
(B) \(\frac{5}{6}\)
(C) \(\frac{11}{12}\)
(D) \(\frac{9}{10}\)
(E) \(\frac{63}{256}\)

Problem 6:

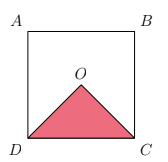
Square \(A B C D\) has centre \(O\).
The shaded area is 16 square units.
What is the length of the side of the square?
(A) 4
(B) 8
(C) 16
(D) 32
(E) 64

Problem 7:

On the number line, which number is halfway between \(10^2\) and \(10^4\) ?
(A) 500
(B) 550
(C) 1010
(D) 2021
(E) 5050

Problem 8:

To feed a horse, Kim mixes three bags of oats with one bag containing \(20 \%\) lucerne and \(80 \%\) oats. If all the bags have the same volume, what percentage of the combined feed mixture is lucerne?
(A) 3
(B) 5
(C) 6
(D) 20
(E) 60

Problem 9:

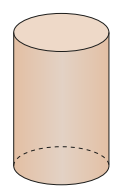
I have a solid block of wood in the shape of a cylinder. The top and bottom faces meet the curved side at right angles. Suppose that I slice the cylinder along a plane to create two smaller blocks of wood.
Which of the following could not be the shape of the resulting faces created by the slice?

Problem 10:

Diya timed herself cycling laps around her suburb. After five laps, her stopwatch indicated a time of 18 minutes and 15 seconds.
What was Diya's average time per lap?
(A) 3 minutes and 3 seconds
(B) 3 minutes and 15 seconds
(C) 3 minutes and 27 seconds
(D) 3 minutes and 39 seconds
(E) 3 minutes and 51 seconds

Problem 11:

I have four consecutive odd numbers. The largest is one less than twice the smallest.
Which of the following is the largest of the four numbers?
(A) 9
(B) 11
(C) 13
(D) 15
(E) 21

Problem 12:

On a compact disc, uncompressed music data is stored as 44100 samples for each second of music, where each sample requires 4 bytes of data. Which of the following is closest to the number of bytes required to store 5 minutes of music on the disc?
(A) 1 million
(B) 5 million
(C) 10 million
(D) 50 million
(E) 100 million

Problem 13:

In the figure, the value of \(x\) is
(A) 30
(B) 40
(C) 50
(D) 60
(E) 70

Problem 14:

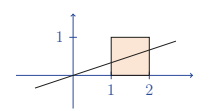
What is the equation of the line passing through \((0,0)\) that bisects the square in the diagram?
(A) \(y=\frac{x}{3}\)
(B) \(y=\frac{x}{2}\)
(C) \(y=\frac{x}{4}\)
(D) \(y=2 x\)
(E) \(y=3 x\)

Problem 15:

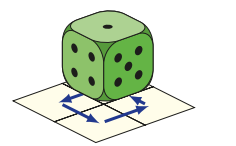
A standard dice numbered 1 to 6 with opposite sides adding to 7 is placed on a 2 by 2 square as shown.
The dice is rolled over one edge onto each of the four base squares in turn and then back on to the original square, as indicated by the arrows.
Which side of the dice is now facing upwards?

Problem 16:

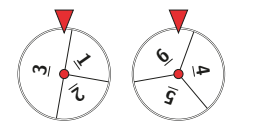
The two spinners shown are spun and the numbers that the arrows point to when they stop are recorded.
For example, the numbers here are 3 and 6. What is the probability that the sum of the two numbers is even?\(A\) \(\frac{1}{2}\)
(B) \(\frac{3}{8}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{2}{3}\)
(E) \(\frac{5}{12}\)

Problem 17:

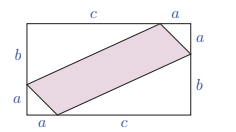
The area of the shaded region is given by
(A) \(a b+a c\)
(B) \(a \sqrt{b^2+c^2}\)
(C) \(b c+a^2-a b-a c\)
(D) \(a b+a c-b c\)
(E) \(a b+a c-a^2\)

Problem 18:

If (k) and \(n\) are positive integers, and \(\sqrt{10 n+k}=k\), then the smallest possible value for \(k\) is
(A) 3
(B) 4
(C) 5
(D) 6
(E) 10

Problem 19:

Two squares are drawn as shown.
The smaller square covers \(\frac{1}{8}\) of the larger square and the larger square covers \(\frac{2}{9}\) of the smaller square.
What is the ratio of the side length of the larger square to the side length of the smaller square?
(A) \(3: 2\)
(B) \(7: 3\)
(C) 7:4
(D) \(5: 3\)
(E) \(4: 3\)

Problem 20:

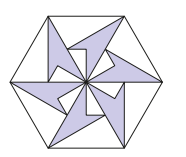
Six identical darts fit inside a regular hexagon as shown. Each dart has three interior angles of \(30^{\circ}\), and one of \(270^{\circ}\). What fraction of the large hexagon is shaded?
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{5}\)
(D) \(\frac{4}{9}\)
(E) \(\frac{3}{8}\)

Problem 21:

We want to place numbers into each of the blank squares in this diagram so that each of the numbers we place is the average of those in the squares directly connected to it. What number should we put in the middle square of the top row?
(A) \(\frac{5}{3}\)
(B) \(\frac{3}{2}\)
(C) \(\frac{10}{9}\)
(D) \(\frac{11}{9}\)
(E) \(\frac{11}{6}\)

Problem 22:

To set the timer on his microwave oven, Rick enters the digits of the hours, minutes and seconds in order from left to right. For example, entering '12345' sets the timer to 1 hour 23 minutes 45 seconds, while entering ' 408 ' sets it to 4 minutes 8 seconds. One day, Rick accidentally missed the last digit and the timer finished 4 minutes and 42 seconds earlier than he was expecting. What was the missing digit?
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7

Problem 23:

I build a large cube from unit cubes. Then I completely paint a number of faces of the large cube. When I dismantle the large cube, I find that I have 288 unit cubes without any paint on them. How many faces of the large cube were painted?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

Problem 24:

The product \(\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)\left(1-\frac{1}{4^2}\right) \cdots\left(1-\frac{1}{15^2}\right)\) is equal to

(A) \(\frac{7}{13}\)
(B) \(\frac{8}{15}\)
(C) \(\frac{9}{16}\)
(D) \(\frac{10}{21}\)
(E) \(\frac{13}{24}\)

Problem 25:

Three artificial islands Razz, Sazz and Tazz were constructed in a shallow sea, each with a coastline of 12 km .

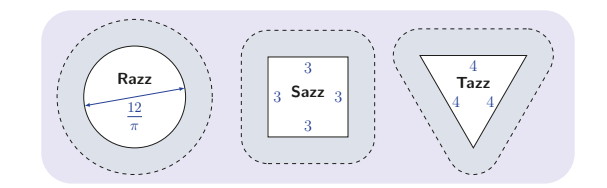
Around each island is a fishing zone, consisting of all points in the sea within 1 km of the island. Which islands have a fishing zone of the largest area?
(A) Razz only
(B) Sazz only
(C) Tazz only
(D) Sazz and Tazz
(E) All three have the same area

Problem 26:

In Australian Rules football, a team scores six points for a 'goal' and one point for a 'behind'. During a game, Vladislav likes to record his team's score with a sequence of sixes and ones. There are exactly three distinct sequences which give a final score of 7 points, namely 6,1 and 1,6 and \(1,1,1,1,1,1,1\).
How many different sequences give a final score of 20 points?

Problem 27:

What is the smallest natural number \(n\) such that the number

\[N=100000 \times 100002 \times 100006 \times 100008+n\]

is a perfect square?

Problem 28:

I have a large supply of matchsticks in four colours: red, yellow, blue and green. I use them to make squares where each side is one matchstick long.
I count two squares as the same if one can be rotated and/or reflected to match the shape and colour of the other.
How many different squares can be created?

Problem 29

Bluey divides the number 499 by each of the numbers \(1,2,3, \ldots, 499\) and records the remainders in order. So her sequence begins:\[0,1,1,3,4,1, \ldots\]Let \(M\) be the sum of these 499 remainders.
Jean-Luc divides the number 500 by each of the numbers \(1,2,3, \ldots, 500\) and records the remainders in order. So his sequence begins:\[0,0,2,0,0,2, \ldots\]Let \(N\) be the sum of these 500 remainders.
What is the difference between the numbers \(M\) and \(N\) ?

Problem 30:

Tyler has a large number of square tiles, all the same size. He has four times as many blue tiles as red tiles. He builds a large rectangle using all the tiles, with the red tiles forming a boundary 1 tile wide around the blue tiles.
He then breaks up this rectangle and uses the tiles to make two smaller rectangles. Like the large rectangle, each of the smaller rectangles has four times as many blue tiles as red tiles, and the red tiles form a boundary 1 tile wide around the blue tiles.
How many blue tiles does Tyler have?