Australian Mathematics Competition - 2020 - Intermediate - Grade 9 & 10 - Questions and Solutions

Problem 1:

\(2-(0-(2-0))=\)

(A) -4
(B) -2
(C) 0
(D) 2
(E) 4

Problem 2:

\(1000 \%\) of 2 is equal to
(A) 0.002
(B) 20
(C) 200
(D) 1002
(E) 2000

Problem 3:

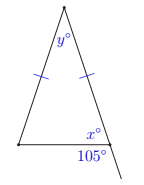
In the diagram provided, find the sum of \(x\) and \(y\).
(A) 30
(B) 75
(C) 95
(D) 105
(E) 180

Problem 4:

\(\frac{1+2+3+4+5}{1+2+3+4}-\frac{1+2}{1+2+3}=\)

(A) 3
(B) \(\frac{5}{6}\)
(C) 1
(D) \(\frac{7}{6}\)
(E) 2

Problem 5:

Sebastien is thinking of two numbers whose sum is 26 and whose difference is 14. The product of Sebastien's two numbers is
(A) 80
(B) 96
(C) 105
(D) 120
(E) 132

Problem 6:

Which of the shapes in the diagram have equal area?
(A) All of the shapes have equal area.
(B) Only Q and S have equal area.
(C) Only R and T have equal area.
(D) Only \(\mathrm{P}, \mathrm{R}\) and T have equal area.
(E) \(\mathrm{P}, \mathrm{R}\) and T have equal area, and Q and S have equal area.

Problem 7:

\(123456-12345+1234-123+12-1=\)

(A) 33333
(B) 101010
(C) 111111
(D) 122223
(E) 112233

Problem 8:

If \(\frac{4}{5}\) of \(\frac{5}{6}\) of \(\frac{\star}{7}\) of \(\frac{7}{8}\) is equal to 1 , then the value of \(\star\) is
(A) 6
(B) 8
(C) 10
(D) 12
(E) 14

Problem 9:

A piece of paper is folded twice as shown and cut along the dotted lines.

Once unfolded, which letter does the piece of paper most resemble?
(A) M
(B) O
(C) N
(D) B
(E) V

Problem 10:

An equilateral triangle is subdivided into a number of smaller equilateral triangles, as shown. The shaded triangle has side length 2. What is the perimeter of the large triangle?
(A) 24
(B) 27
(C) 30
(D) 33
(E) 36

Problem 11:

Triangle \(X Y S\) is enclosed by rectangle \(P Q R S\) as shown in the diagram. In square centimetres, what is the area of triangle \(X Y S\) ?
(A) 82
(B) 88
(C) 94
(D) 112
(E) 130

Problem 12:

Let \(X=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11}\) and \(Y=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}\). Then \(X-Y\) is equal to
(A) \(\frac{2}{99}\)
(B) \(\frac{1}{11}\)
(C) \(\frac{1}{10}\)
(D) \(\frac{1}{2}\)
(E) \(\frac{2}{9}\)

Problem 13:

The number 25 can be written as the sum of three different primes less than 20. For instance, \(25=5+7+13\).
How many multiples of 10 can be written as the sum of three different primes less than 20?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

Problem 14:

In this circle with centre \(O\), four triangles are drawn, with angles as shown.
What is the value of \(x\) ?
(A) 10
(B) 15
(C) 18
(D) 24
(E) 36

Problem 15:

There are 10 children in a classroom. The ratio of boys to girls increases when another girl and another boy enter the room. What is the greatest number of boys that could have been in the room at the beginning?
(A) 1
(B) 4
(C) 5
(D) 6
(E) 9

Problem 16:

Two triangles, \(A\) and \(B\), have the same area. Triangle \(A\) is isosceles and triangle \(B\) is right-angled.

The difference between the perimeters of triangle \(A\) and triangle \(B\) is
(A) nothing
(B) between 0 cm and 1 cm
(C) between 1 cm and 2 cm
(D) between 2 cm and 3 cm
(E) more than 3 cm

Problem 17:

A list of numbers has first term 2 and second term 5. The third term, and each term after this, is found by multiplying the two preceding terms together: \(2,5,10,50,500, \ldots\). The value of the eighth term is
(A) \(2^5 \times 5^8\)
(B) \(2^8 \times 5^9\)
(C) \(2^8 \times 5^{13}\)
(D) \(2^9 \times 5^{15}\)
(E) \(2^{13} \times 5^{21}\)

Problem 18:

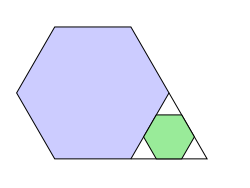
Two sides of a regular hexagon are extended to create a small triangle.
Inside this triangle, a smaller regular hexagon is drawn, as shown. In area, how many times bigger is the larger hexagon than the smaller hexagon?
(A) 4
(B) 6
(C) 8
(D) 9
(E) 12

Problem 19:

The number \(\frac{1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9 \times 10}{n}\) is a perfect square.
What is the smallest possible value of \(n\) ?
(A) 7
(B) 14
(C) 21
(D) 35
(E) 70

Problem 20:

In the triangle \(A B C\) shown, \(D\) is the midpoint of \(A C, E\) is the midpoint of \(B D\) and \(F\) is the midpoint of \(A E\). If the area of triangle \(B E F\) is 5 , what is the area of \(\triangle A B C\) ?
(A) 30
(B) 35
(C) 40
(D) 45
(E) 50

Problem 21:

A scientist measured the amount of bacteria in a Petri dish over several weeks and also recorded the temperature and humidity for the same time period. The results are summarised in the following graphs.

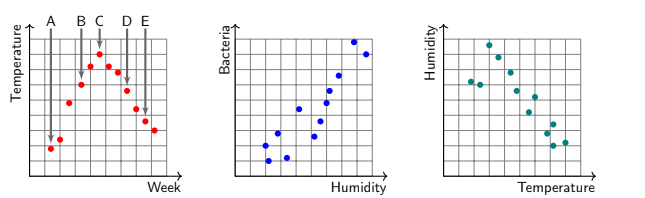
During which week was the bacteria population highest?
(A) week A
(B) week B
(C) week C
(D) week D
(E) week E

Problem 22:

Five friends read a total of 40 books between them over the holidays. Everyone read at least one book but no-one read the same book as anyone else. Asilata read twice as many books as Eammon. Dane read twice as many as Bettina. Collette read as many as Dane and Eammon put together. Who read exactly eight books?
(A) Asilata
(B) Bettina
(C) Colette
(D) Dane
(E) Eammon

Problem 23:

There are 5 sticks of length \(2 \mathrm{~cm}, 3 \mathrm{~cm}, 4 \mathrm{~cm}, 5 \mathrm{~cm}\) and 8 cm . Three sticks are chosen randomly. What is the probability that a triangle can be formed with the chosen sticks?
(A) 0.25
(B) 0.3
(C) 0.4
(D) 0.5
(E) 0.6

Problem 24:

Five squares of unit area are circumscribed by a circle as shown. What is the radius of the circle?
(A) \(\frac{3}{2}\)
(B) \(\frac{2 \sqrt{5}}{3}\)
(C) \(\frac{\sqrt{10}}{2}\)
(D) \(\frac{\sqrt{13}}{2}\)
(E) \(\frac{\sqrt{185}}{8}\)

Problem 25:

Alex writes down the value of the following sum, where the final term is the number consisting of 2020 consecutive nines:

How many times does the digit 1 appear in the answer?
(A) 0
(B) 2016
(C) 2018
(D) 2020
(E) 2021

Problem 26:

If \(n\) is a positive integer, (n) ! is found by multiplying the integers from 1 to \(n\). For example, \(4!=4 \times 3 \times 2 \times 1=24\). What are the three rightmost digits of the sum \(1!+2!+3!+\cdots+2020!\)?

Problem 27:

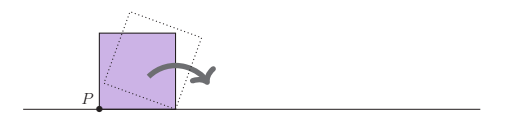
A square of side length 10 cm is sitting on a line. Point \(P\) is the corner of the square which starts at the bottom left, as shown. Without slipping, the square is rolled along the line in a clockwise direction until \(P\) returns to the line for the first time. To the nearest square centimetre, what is the area under the curve traced by \(P\)?

Problem 28:

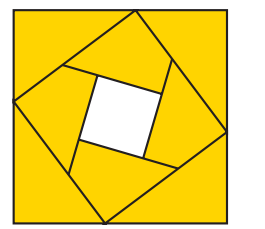
Eight identical right-angled triangles with side lengths \(30 \mathrm{~cm}, 40 \mathrm{~cm}\) and 50 cm are arranged as shown. The inner four triangles are made to overlap each other, but the outer four triangles do not overlap any of the others.
What is the area, in square centimetres, of the unshaded centre square?

Problem 29:

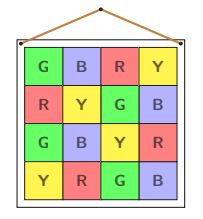
My grandson makes wall hangings by stitching together 16 square patches of fabric into a \(4 \times 4\) grid. I asked him to use patches of red, blue, green and yellow, but to ensure that no patch touches another of the same colour, not even diagonally. The picture shows an attempt which fails only because two yellow patches touch diagonally. In how many different ways can my grandson choose to arrange the coloured patches correctly?

Problem 30:

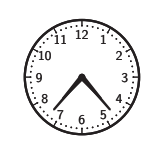
A clockmaker makes a 12-hour clock but with the hour and minute hands identical. An ambiguous time on this clock is one where you cannot tell what time it is, since the exact position of the two hands occurs twice in a 12-hour cycle. For instance, the clock shown can be seen at approximately 7.23 pm and 4.37 pm so both of these times are ambiguous. However, 12.00 pm is not ambiguous, since both hands are together. How many ambiguous times happen in the 12 hours from midday to midnight?