Australian Mathematics Competition - 2019 - Junior years - Grade 7 & 8 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free Resources\(201-9= \)
(A) 111
(B) 182
(C) 188
(D) 192
(E) 198
This rectangle is 5 cm wide and 4 cm tall. What is its area in square centimetres?
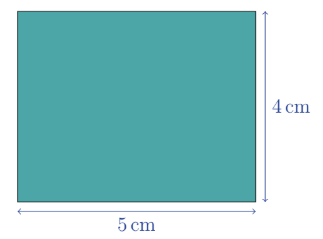
(A) 9
(B) 10
(C) 18
(D) 20
(E) 40
The table shows the number of boys and girls aged 10 or 11 in year 5. How many boys aged 11 are in year 5 ?
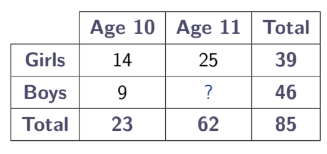
(A) 9
(B) 11
(C) 21
(D) 37
(E) 46
The table shows the number of boys and girls aged 10 or 11 in year 5. How many boys aged 11 are in year 5?
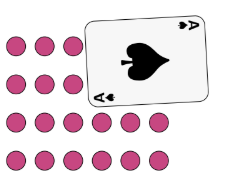
(A) 9
(B) 11
(C) 21
(D) 37
(E) 46
Which one of the following is the largest number?
(A) 4.05
(B) 4.45
(C) 4.5
(D) 4.045
(E) 4.54
What is \(25 \%\) of \(\frac{1}{2}\)?
(A) \(\frac{1}{16}\)
(B) \(\frac{1}{8}\)
(C) \(\frac{1}{4}\)
(D) 1
(E) 2
Problem 7:
We're driving from Elizabeth to Renmark, and as we leave we see this sign. We want to stop at a town for lunch and a break, approximately halfway to Renmark. Which town is the best place to stop?

(A) Gawler
(B) Nuriootpa
(C) Truro
(D) Blanchetown
(E) Waikerie
Problem 8:
This letter F is first rotated by \(90^{\circ}\) clockwise and then reflected in a horizontal line. It will now look like this.
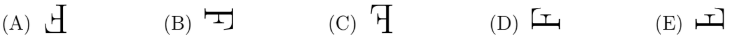
Problem 9:
Edith wrote down the whole numbers from 1 to 20 on a piece of paper. How many times did she write the digit 1?
(A) 9
(B) 10
(C) 11
(D) 12
(E) 13
Problem 10:
Danny divided a whole number \(P\) by another whole number \(Q\) on his calculator and got the answer 3.125.
Later, Danny forgot the two whole numbers, but he knew that both were under 30 . The value of \(Q\) is
(A) 5
(B) 7
(C) 8
(D) 10
(E) 25
Problem 11:
Every row and every column of this \(3 \times 3\) square must contain each of the numbers 1,2 and 3. What is the value of \(N+M\)?
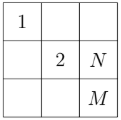
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
Problem 12:
A piece of paper is folded in three, then a semi-circular cut and a straight cut are made, as shown in the diagram.

When the paper is unfolded, what does it look like?

Problem 13:
What is the value of z?
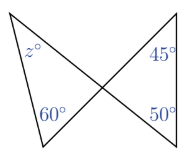
(A) 30
(B) 35
(C) 45
(D) 50
(E) 55
Problem 14:
\(\frac{1111111111}{111}=\)
(A) 11111
(B) 1001001
(C) 10001
(D) 10101
(E) 1001
Problem 15:
Jill has the same number of brothers as she has sisters. Her brother Jack has twice as many sisters as he has brothers. How many children are in the family?
(A) 4
(B) 5
(C) 7
(D) 9
(E) 11
Problem 16:
The large rectangle shown has been divided into 6 smaller rectangles. The shaded rectangle in the bottom-right corner has dimensions of \(2 \mathrm{~cm} \times 3 \mathrm{~cm}\). The remaining five rectangles all have the long side equal to twice the short side. The smallest of these has a width of 1 cm .
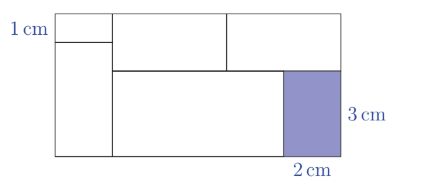
What is the total area of the original large rectangle, in square centimetres?
(A) 42
(B) 44
(C) 50
(D) 56
(E) 70
Problem 17:
In my dance class, 14 students are taller than Bob, and 12 are shorter than Alice. Four students are both shorter than Alice and taller than Bob. How many students are in my dance class?
(A) 22
(B) 24
(C) 26
(D) 28
(E) 30
Problem 18:
My washing machine has a digital display. It counts down the time remaining until the end of the wash, although sometimes I confuse the time remaining with the actual time. At 1.05 pm yesterday the washing machine displayed 2:41, namely 2 hours and 41 minutes remaining. When did the washing machine's countdown display happen to agree with the actual time?

(A) 2.41 pm
(B) 3.46 pm
(C) 2.23 pm
(D) 1.36 pm
(E) 1.53 pm
Problem 19:
A seven-digit number is in the form (20 A M C 19), with all digits different. It is divisible by 9.
What is the value of (A+M+C)?
(A) 6
(B) 9
(C) 12
(D) 15
(E) 18
Problem 20:
John, Chris, Anne, Holly, Mike and Norman are seated around a round table, each with a card with a number on it in front of them. Each person can see the numbers in front of their two neighbours, and says the sum of these two numbers. John says 30, Chris says 33, Anne says 32, Holly says 38, Mike says 36 and Norman says 41. What number does Holly have in front of her?

(A) 17
(B) 18
(C) 19
(D) 23
(E) 37
Problem 21:
On this simple system of roads, how many ways are there to get from \(A\) to \(B\) without visiting any of the 9 intersections more than once?
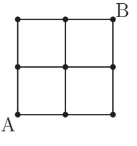
(A) 8
(B) 10
(C) 12
(D) 14
(E) 16
Problem 22:
The average time for a class of 30 mathematics students to travel to school is 21 minutes. The boys' average is 25 minutes and the girls' average is 19 minutes. How many boys are in the class?
(A) 10
(B) 12
(C) 14
(D) 15
(E) 18
Problem 23:
A \(4 \mathrm{~cm} \times 4 \mathrm{~cm}\) board can have \(1 \mathrm{~cm}^3\) cubes placed on it as shown. The board is cleared, then a number of these cubes are placed on the grid. The front and right side views are shown.

What is the maximum number of cubes there could be on the board?

(A) 10
(B) 11
(C) 16
(D) 17
(E) 18
Problem 24:
Three athletes Andy, Bob and Chase took part in a 100-metre race, each running at a constant speed. Andy won the race in 10 seconds. When Andy crossed the finish line, Bob was 10 metres behind. When Bob crossed the finish line, Chase was 10 metres behind Bob. When Andy crossed the finish line, how far behind was Chase?
(A) 21 m
(B) 20 m
(C) 19 m
(D) 18 m
(E) 17 m
Problem 25:
Seven squares and two equilateral triangles, all with the same side lengths, are used to form the 3-dimensional 'house shape' shown.

Which of the following diagrams does not show a net which can be created by cutting along some of the edges and folding the shape flat?

Problem 26:
A tower is built from exactly 2019 equal rods. Starting with 3 rods as a triangular base, more rods are added to form a regular octahedron with this base as one of its faces. The top face is then the base of the next octahedron. The diagram shows the construction of the first three octahedra. How many octahedra are in the tower when it is finished?

Problem 27:
A positive whole number is called stable if at least one of its digits has the same value as its position in the number. For example, 78247 is stable because a 4 appears in the \(4^{\text {th }}\) position. How many stable 3-digit numbers are there?
Problem 28:
When I divide an integer by 15, the remainder is an integer from 0 to 14 . When I divide an integer by 27, the remainder is an integer from 0 to 26. For instance, if the integer is 100 then the remainders are 10 and 19, which are different. How many integers from 1 to 1000 leave the same remainders after division by 15 and after division by 27?
Problem 29:
In a list of numbers, an odd-sum triple is a group of three numbers in a row that add to an odd number. For instance, if we write the numbers from 1 to 6 in this order,
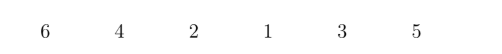
then there are exactly two odd-sum triples: \((4,2,1)\) and \((1,3,5)\). What is the greatest number of odd-sum triples that can be made by writing the numbers from 1 to 1000 in some order.
Problem 30:
The Leader of Zip decrees that the digit 0, since it represents nothing, will no longer be used in any counting number. Only counting numbers without 0 digits are allowed. So the counting numbers in Zip begin \(1,2,3,4,5,6,7,8,9,11,12, \ldots\), where the tenth counting number is 11. When you write out the first one thousand allowable counting numbers in Zip, what are the last three digits of the final number?