Australian Mathematics Competition - 2016 - Upper Primary - Grade 5 & 6 - Questions and Solutions

Problem 1:

Which of these numbers is the smallest?
(A) 655
(B) 566
(C) 565
(D) 555
(E) 556

Problem 2:

Two pizzas are sliced into quarters. How many slices will there be?
(A) 2
(B) 10
(C) 6
(D) 8
(E) 16

Problem 3:

Join the dots \(P, Q, R\) to form the triangle \(P Q R\).

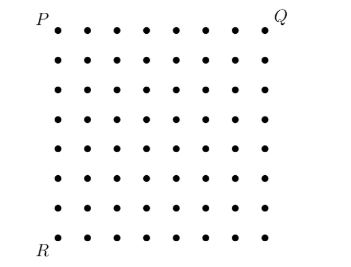
How many dots lie inside the triangle \(P Q R\) ?
(A) 13
(B) 14
(C) 15
(D) 17
(E) 18

Problem 4:

\(0.3+0.4\) is
(A) 0.07
(B) 0.7
(C) 0.12
(D) 0.1
(E) 7

Problem 5:

Lee's favourite chocolates are 80 c each. He has five dollars to spend. How many of these chocolates can he buy?
(A) 4
(B) 5
(C) 6
(D) 7
(E) 8

Problem 6:

Ten chairs are equally spaced around a round table. They are numbered 1 to 10 in order. Which chair is opposite chair 9 ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

Problem 7:

In a piece of music, a note like is worth one beat, is worth half a beat, is worth
2 beats and is worth 4 beats. How many beats are in the following piece of music?

(A) 4
(B) 5
(C) 6
(D) 7
(E) 8

Problem 8:

Phoebe put her hand in her pocket and pulled out 60 cents. How many different ways could this amount be made using \(10 \mathrm{c}, 20 \mathrm{c}\) and 50 c coins?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6

Problem 9:

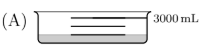
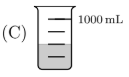
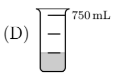
Which of these containers is currently holding the most water?

Problem 10:

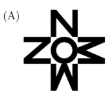
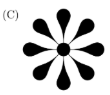
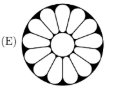
Which of these shapes has the most axes of symmetry (mirror lines)?

Problem 11:

A sailor coiled a rope on his ship's deck, and some paint was spilled across half of it. What did the rope look like when it was uncoiled?

Problem 12:

If the area of the tangram shown is 64 square centimetres, what is the area in square centimetres of the small square?
(A) 32
(B) 24
(C) 16
(D) 8
(E) 4

Problem 13:

For each batch of 25 biscuits, Jack uses \(2 \frac{1}{2}\) packets of chocolate chips. How many packets does he need if he wants to bake 200 biscuits?
(A) 20
(B) 8
(C) 80
(D) 10
(E) 50

Problem 14:

Which one of the following is correct?
(A) Two even numbers add to an odd number.
(B) An odd number minus an odd number is always odd.
(C) Adding 2 odd numbers and an even number is always odd.
(D) Adding 3 odd numbers is always odd.
(E) An odd number multiplied by an odd number always equals an even number.

Problem 15:

The perimeter of the outer square is 36 cm , and the perimeter of the inner square is 20 cm .
If the four rectangles are all identical, what is the perimeter of the shaded rectangle in centimetres?
(A) 12
(B) 14
(C) 24
(D) 20
(E) 18

Problem 16:

George has a new lock that opens if the four numbers \(1,2,3\) and 4 are pressed once each in the correct order.
If the first number must be larger than the second number, how many combinations are possible?
(A) 10
(B) 12
(C) 15
(D) 18
(E) 20

Problem 17:

A straight cut is made through the hexagon shown to create two new shapes. Which of the following could not be made?
(A) one triangle and one hexagon
(B) two pentagons
(C) two quadrilaterals
(D) one quadrilateral and one pentagon
(E) one triangle and one quadrilateral

Problem 18:

The numbers \(3,9,15,18,24\) and 29 are divided into two groups of 3 numbers and each group is added. The difference between the two sums (totals) of 3 numbers is as small as possible. What is the smallest difference?
(A) 0
(B) 1
(C) 2
(D) 5
(E) 8

Problem 19:

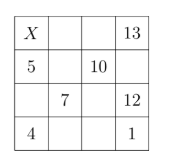
Benny built a magic square using the numbers from 1 to 16 , where the numbers in each row, each column and each diagonal add up to the same total.
What number does he place at the X ?
(A) 16
(B) 15
(C) 17
(D) 11
(E) 14

Problem 20:

Andy has a number of red, green and blue counters.
He places eight counters equally spaced around a circle according to the following rules:

• No two red counters will be next to each other.
• No two green counters will be diagonally opposite each other.
• As few blue counters as possible will be used.

How many blue counters will Andy need to use?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4

Problem 21:

I have five coloured discs in a pile as shown.
I take the top two discs and put them on the bottom (with the red dise still on top of the blue disc).
Then I again take the top two discs and put them on the bottom.
If I do this until I have made a total of 21 moves, which dise will be on the bottom?

(A) red
(B) blue
(C) green
(D) yellow
(E) orange

Problem 22:

A zoo keeper weighed some of the animals at Melbourne Zoo. He found that the lion weighs 90 kg more than the leopard, and the tiger weighs 50 kg less than the lion. Altogether the three animals weigh 310 kg . How much does the lion weigh?
(A) 180 kg
(B) 150 kg
(C) 140 kg
(D) 130 kg
(E) 100 kg

Problem 23:

Adrienne, Betty and Cathy were the only three competitors participating in a series of athletic events. In each event, the winner gets 3 points, second gets 2 points and third gets 1 point. After the events, Adrienne has 8 points, Betty has 11 points and Cathy has 5 points. In how many events did Adrienne come second?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4

Problem 24:

Jane and Tom are comparing their pocket money. Jane has as many 5c coins as Tom has 10 c coins and as many 10 c coins as Tom has 20 c coins. However, Jane has as many 50c coins as Tom has 5 c coins.
They have no other coins and they find that they each have the same amount of money.
What is the smallest number of coins they each can have?
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7

Problem 25:

A tuckshop has two jars of cordial mixture.
Jar A is \(30 \%\) cordial, while Jar B is \(60 \%\) cordial.
Some of Jar A is mixed with some of Jar B to make 18 litres of \(50 \%\) cordial.
How many litres from Jar A are used?
(A) 9
(B) 12
(C) 4
(D) 3
(E) 6

Problem 26:

Qiang, Rory and Sophia are each wearing a hat with a number on it. Each adds the two numbers on the other two hats, giving totals of 11,17 and 22 . What is the largest number on a hat?

Problem 27:

The number 840 is the 3 -digit number with the most factors. How many factors does it have?

Problem 28:

A class has 2016 matchsticks. Using blobs of modelling clay to join the matches together, they make a long row of cubes. This is how their row starts.

They keep adding cubes to the end of the row until they don't have enough matches left for another cube. How many cubes will they make?

Problem 29:

You have an unlimited supply of five different coloured pop-sticks, and want to make as many different coloured equilateral triangles as possible, using three sticks.
One example is shown here.
Two triangles are not considered different if they are rotations or reflections of each other.
How many different triangles are possible?

Problem 30:

Today my three cousins multiplied their ages together and it came to 2016. This day last year their ages multiplied to 1377 .
When they multiplied their ages together 2 years ago today, what was their answer?