Australian Mathematics Competition - 2016 - Intermediate - Grade 9 & 10 - Questions and Solutions
 Join Trial or Access Free Resources
Join Trial or Access Free Resources Join Trial or Access Free Resources
Join Trial or Access Free ResourcesWhat is the value of \(20 \times 16\)?
(A) 320
(B) 140
(C) 2016
(D) 32
(E) 800

In the figure, the shaded region is what fraction of the circle?
(A) \(\frac{1}{20}\)
(B) \(\frac{1}{10}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{60}\)
(E) \(\frac{1}{40}\)
The cycling road race through the Adelaide Hills started at 11:15 am and the winner finished at 2:09 pm the same day. The winner's time in minutes was
(A) 135
(B) 174
(C) 164
(D) 294
(E) 186
The fraction \(\frac{720163}{2016}\) is
(A) between 0 and 1
(B) between 1 and 10
(C) between 10 and 100
(D) between 100 and 1000
(E) greater than 1000
What is the value of \((1 \div 2) \div(3 \div 4\)) ?
(A) \(\frac{2}{3}\)
(B) \(\frac{3}{2}\)
(C) \(\frac{3}{8}\)
(D) \(\frac{1}{6}\)
(E) \(\frac{1}{24}\)
\(0.75 \%\) of a number is 6 . The number is
(A) 800
(B) 300
(C) 1200
(D) 400
(E) 100
In the expression below, the letters \(A, B, C, D\) and \(E\) represent the numbers \(1,2,3,4\) and 5 in some order.
\(A \times B+C \times D+E\)
What is the largest possible value of the expression?
(A) 24
(B) 27
(C) 26
(D) 51
(E) 25
In each of these squares, the marked length is 1 unit. Which of the squares would have the greatest perimeter?

(A) P
(B) Q
(C) R
(D) S
(E) all are the same

On a clock face, a line is drawn between 9 and 3 and another between 12 and 8 . What is the acute angle between these lines?
(A) \(45^{\circ}\)
(B) \(60^{\circ}\)
(C) \(50^{\circ}\)
(D) \(30^{\circ}\)
(E) \(22.5^{\circ}\)
There are 3 blue pens, 4 red pens and 5 yellow pens in a box. Without looking, I take pens from the box one by one. How many pens do I need to take from the box to be certain that I have at least one pen of each colour?
(A) 8
(B) 9
(C) 10
(D) 11
(E) 12

In the diagram, the value of \(x^\circ\) is
(A) 120
(B) 108
(C) 105
(D) 135
(E) 112.5

How far is it from \(A\) to \(B\) measured in a straight line?
(A) 20
(B) 28
(C) \(10+9 \sqrt{2}\)
(D) \(8+9 \sqrt{2}\)
(E) 16

A circle of radius 1 metre is inscribed inside a semicircle of radius 2 metres. What is the area in square metres of the semicircle not covered by the circle?
(A) \(2 \pi\)
(B) \(\pi-1\)
(C) 2
(D) \(2 \pi-1\)
(E) \(\pi\)
The value of (n) for which \(4^{n+1}=2^{10}\) is
(A) 9
(B) 8
(C) 4
(D) 10
(E) 2
Adrienne, Betty and Cathy were the only three competitors participating in a series of athletic events. In each event, the winner gets 3 points, the second gets 2 points and the third gets 1 point. After the events, Adrienne has 8 points, Betty has 11 points and Cathy has 5 points. In how many events did Adrienne come second?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
What is the smallest number \(N\) for which \(\frac{2016}{N}\) is a perfect square?
(A) 14
(B) 2
(C) 56
(D) 12
(E) 7
Five people are sitting around a circle. Some always tell the truth, whilst the others always lie. Each person claims to be sitting between two liars. How many of them are telling the truth?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
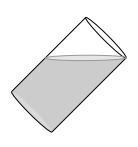
A cylindrical glass of (inside) diameter 6 cm and height 11 cm is filled and then tilted to a \(45^{\circ}\) angle so that some water overflows. How much water is left in it?
(A) \(48 \pi \mathrm{~mL}\)
(B) \(45 \pi \mathrm{~mL}\)
(C) \(66 \pi \mathrm{~mL}\)
(D) \(72 \pi \mathrm{~mL}\)
(E) \(63 \pi \mathrm{~mL}\)
Ten students sit a test consisting of 20 questions. Two students get 8 questions correct and one student gets 9 questions correct. The remaining seven students all get at least 10 questions correct and the average number of questions answered correctly by these seven students is an integer. If the average number of questions answered correctly by all ten students is also an integer, then that integer is
(A) 10
(B) 11
(C) 12
(D) 13
(E) 14

This pedal-powered water pump is made from bicycle parts. A 30-tooth gear on the pedals has a chain to a 15-tooth gear. On the same axle as the 15-tooth gear is a 32-tooth gear that drives a chain to a 40-tooth gear on the pump. For every 100 complete revolutions of the pedals, how many times does the gear on the pump turn?
(A) 160
(B) 250
(C) 107
(D) 93
(E) \(37 \frac{1}{2}\)

A gardener wishes to put a circular water feature (pool) in a right-angled triangular plot that has sides of 6 m and 8 m on its two smallest sides. What is the radius in metres of the largest pool that will fit?
(A) \(2 \sqrt{2}-1\)
(B) 2
(C) 4
(D) 3
(E) \(2 \sqrt{2}\)
A sequence of 10 letters is made according to the following rules.
How many possible sequences are there where the first, fourth, and tenth letters are all Q?
(A) 63
(B) 39
(C) 32
(D) 45
(E) 36
Cynthia's afternoon train normally arrives at her station at \(5: 30 \mathrm{pm}\) each day, where she is picked up by Alan and driven home. One day she was on an earlier train which arrived at 5 pm , and she decided to walk in the direction Alan was coming from home. Alan had left in time to meet the \(5: 30 \mathrm{pm}\) train, but this time he picked up Cynthia and they arrived home 10 minutes earlier than usual. For how many minutes had Cynthia walked before Alan picked her up?
(A) 20
(B) 30
(C) 25
(D) 10
(E) 15

You have an unlimited supply of five different coloured pop-sticks, and want to make as many different coloured equilateral triangles as possible, using three sticks. One example is shown here. Two triangles are not considered different if they are rotations or reflections of each other.
How many different triangles are possible?
(A) 35
(B) 5
(C) 20
(D) 56
(E) 10
A super-Fibonacci sequence is a list of whole numbers with the property that, from the third term onwards, every term is the sum of all of the previous terms. For example, \(1,4,5,10, \ldots\) How many super-Fibonacci sequences starting with 1 involve the number (2016 ?)
(A) 1
(B) 3
(C) 5
(D) 7
(E) 9
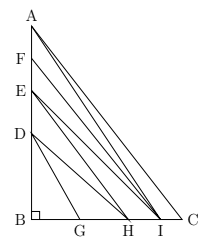
The right-angled triangle \(A B C\) has area \(2016 \mathrm{~cm}^2\). Lines \(A I, I F, I E, E H, H D, D G\) divide the large triangle into seven smaller triangles of equal area. If (\triangle B I E) is an isosceles triangle, find the length of \(B G\) in centimetres.

A symmetrical cross with equal arms has an area of \(2016 \mathrm{~cm}^2\) and all sides of integer length in centimetres. What is the smallest perimeter the cross can have, in centimetres?
The ten students in Malcolm's maths class all took a test. The scores of the other nine students were (82,83,85,89,90,92,95,97), and 98 , and Malcolm's score was a whole number. The teacher had made a mistake in calculating Malcolm's score. After she corrected her mistake, both the mean and the median of all the scores increased by 0.5 . There are two possible correct scores that Malcolm could have had. What is the sum of these two scores?
A high school marching band can be arranged in a rectangular formation with exactly three boys in each row and exactly five girls in each column. There are several sizes of marching band for which this is possible. What is the sum of all such possible sizes?

Around a circle, I place 64 equally spaced points, so that there are \(64 \times 63 \div 2=2016\) possible chords between these points. I draw some of these chords, but each chord cannot cut across more than one other chord. What is the maximum number of chords I can draw?