Australian Mathematics Competition - 2008 - Middle Primary - Grade 3 & 4 - Questions and Solutions

Problem 1:

Which number is one hundred more than the number $765 ?$
(A) 865
(B) 985
(C) 876
(D) 775
(E) 766

Problem 2:

What time is shown on the clock below?

(A) 8:00
(B) 9:30
(C) 6:30
(D) 8:30
(E) 8:40

Problem 3:

What fraction of the diagram below has been shaded?

(A) $\frac{1}{3}$
(B) $\frac{4}{3}$
(C) $\frac{3}{4}$
(D) $\frac{1}{4}$
(E) $\frac{3}{1}$

Problem 4:

Wendy has 20 marbles. She has five times as many marbles as Jim. How many marbles does Jim have?
(A) 4
(B) 100
(C) 5
(D) 25
(E) 15

Problem 5:

A string of coloured beads begins with a red, then a green, then a blue, then a yellow. This pattern is repeated many times. What colour is the 26th bead?
(A) red
(B) green
(C) blue
(D) yellow
(E) white

Problem 6:

On Sue's 5th birthday, her brother Joe was 8 years old. How old will Joe be on Sue's 10th birthday?
(A) 16
(B) 15
(C) 13
(D) 12
(E) 11

Problem 7:

In the diagram, the arrow ' $\longrightarrow$ ' means 'is half of'. For example,

(A) 2
(B) 32
(C) 4
(D) 16
(E) 64

Problem 8:

A park needs seven new picnic tables, each with a top and two seats. The tops are each made from four boards and each seat is made from two boards.

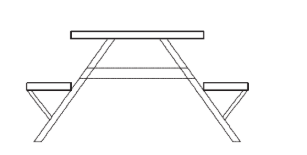
How many boards does the park manager need to order?
(A) 66
(B) 35
(C) 60
(D) 70
(E) 56

Problem 9:

A cyclist rides 25 kilometres every day for a week. If he starts on a Monday, by what day would he have ridden 60 kilometres?
(A) Tuesday
(B) Wednesday
(C) Thursday
(D) Friday
(E) Saturday

Problem 10:

In the number sentence

$$
10 \text { hundreds }+100 \text { tens }= tens,
$$

What number goes in the box to make it true?
(A) 100
(B) 20
(C) 110
(D) 200
(E) 1000

Problem 11:

Jenny has three boxes, each having the same number of toy cars inside. She finds two more cars down the back of the sofa. When she counts all her cars she finds that she has 17 . How many cars are there in each box?
(A) 3
(B) 5
(C) 6
(D) 8
(E) 15

Problem 12:

Three drips make two drops. How many drips make 18 drops?
(A) 6
(B) 12
(C) 27
(D) 36
(E) 48

Problem 13:

A box holds socks which are all the same size. There are 6 white, 10 blue and 16 grey socks. What is the least number of socks I need to take out, without looking, so that I can be certain of getting a pair of matching socks?
(A) 3
(B) 4
(C) 5
(D) 6
(E) 10

Problem 14:

In the number sentence,

what number do we put in the $\square$ to make the number sentence true?
(A) 2
(B) 4
(C) 8
(D) 16
(E) 40

Problem 15:

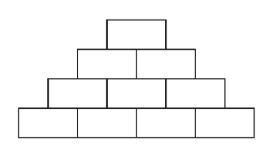
There is a stack of 45 blocks with one block on top, 2 blocks in the next row, 3 in the next row and so on. How many blocks are in the bottom row and how many rows are there?

(A) 9 blocks and 10 rows
(B) 10 blocks and 10 rows
(C) 8 blocks and 8 rows
(D) 6 blocks and 9 rows
(E) 9 blocks and 9 rows

Problem 16:

Annie leaves home at 9:15 am to walk to Derek's house, which takes her 25 minutes. Carl leaves his house 5 minutes after Annie but only takes 6 minutes to get to Derek's house. When Carl arrives, how long, in minutes, will he and Derek have to wait for Annie to arrive?

(A) 6
(B) 11
(C) 14
(D) 21
(E) 24

Problem 17:

At half-time in a soccer match between Newcastle and Melbourne, the score was Newcastle 1, Melbourne 0 . Three goals were scored in the second half. Which of the following could not be the result of the match?

(A) The match was drawn
(B) Newcastle won by 2 goals
(C) Melbourne won by 2 goals
(D) Newcastle won by 1 goal
(E) Newcastle won by 4 goals

Problem 18:

A 1 metre square of cardboard is cut up into 1 cm by 1 cm squares. If these squares were laid side by side, what distance would they cover?
(A) 1000 cm
(B) 200 m
(C) 20 m
(D) 100 m
(E) 100 cm

Problem 19:

I have three rectangular tiles, which are 2 cm by $1 \mathrm{~cm}, 3 \mathrm{~cm}$ by 1 cm and 4 cm by 1 cm .

If I put them together so that they do not overlap, but touch along edges, what is the smallest possible perimeter of their combined shape?
(A) 14 cm
(B) 16 cm
(C) 18 cm
(D) 20 cm
(E) 24 cm

Problem 20:

Lying Larry decided that from now on he is going to tell the truth on Mondays, Wednesdays and Fridays, but will lie on all the other days. Once, he said 'Tomorrow I am going to tell the truth.' On what day did this happen?
(A) Saturday
(B) Friday
(C) Sunday
(D) Wednesday
(E) Monday

Problem 21:

If four days after the day before yesterday was Saturday, what day will tomorrow be?
(A) Saturday
(B) Wednesday
(C) Sunday
(D) Thursday
(E) Friday

Problem 22:

In a group of students, 14 collect stamps, 16 collect postcards, 5 collect both but 4 collect neither. How many students are in the group?
(A) 39
(B) 34
(C) 29
(D) 35
(E) 64

Problem 23:

In the $5 \times 5$ square below, the numbers $1,2,3,4$ and 5 are to be placed in the squares so that each number appears exactly once in each row and once in each column. Some numbers have already been placed.

When the square is completed, the number which is in the square marked with an X is
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

Problem 24:

I have some animals, an equal number of goats and lions, which I wish to ferry across a river but my boat will allow me to take only one animal at a time. I cannot leave one goat on its own on either side nor can I leave 1 goat with 1 lion (but I can leave 2 or more goats with a lion or 2 or more lions with a goat). What is the smallest number of goats such that I can ferry the group across without breaking these restrictions?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6

Problem 25:

The desks in Amy's classroom are arranged in five rows of five, equally spaced apart. Amy's friend Sam sits in the opposite corner to her. How many people are closer to Sam than they are to Amy?
(A) 8
(B) 9
(C) 11
(D) 12
(E) 14

Problem 26:

In a circle dance, everyone is evenly spaced around a circle and has a number in the order $1,2,3,4,5, \ldots$, and so on. The dancer with number 15 is directly opposite dancer number 3 . How many dancers are in the circle?

Problem 27:

A theatre sets up its chairs in equal rows. Alison had a seat which was third from the front and 18th from the back. Naida could see 8 chairs to her left and 11 to her right. How many chairs are in the theatre?

Problem 28:

Jim takes an hour to fold the weekly washing for the whole family. His older sister Susan can do the same job in half the time. How many minutes would it take them to fold the washing together if they continue to fold at their own rates?

Problem 29:

What is the largest number less than 1000 , which is odd, leaves a remainder of 2 when divided by 3 , and a remainder of 4 when divided by 5 ?

Problem 30:

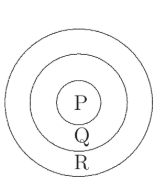
Anne designs the dart board shown, where she scores $P$ points in the centre circle, $Q$ points in the next ring and $R$ points in the outer ring. She throws three darts in each turn. In her first turn, she gets two darts in ring $Q$ and one in ring $R$ and scores 10 points. In her second turn, she gets two in circle $P$ and one in ring $R$ and scores 22 points.
In her next turn, she gets one dart in each of the regions. How many points does she score?