Let \(x=2^{300}, y=3^{200}\) and \(z=6^{100}\). Which of the following is true?
(A) \(x>y>z\)
(B) \(x>z>y\)
(C) \(y>z>x\)
(D) \(y>x>z\)
(E) \(z>x>y\)
An expensive painting was stolen and the police rounded up five suspects Alfred, Boris, Chucky, Dan and Eddie. These were the statements that were recorded.
Alfred: "Either Boris or Dan stole the painting."
Boris: "I think Dan or Eddie is the guilty party."
Chucky: "It must be Dan."
Dan: "Boris or Eddie did it!"
Eddie: "I am absolutely sure the thief is Alfred."
The police knew that only one of the five suspects stole the painting and that all five were lying. Who stole the painting?
(A) Alfred
(B) Boris
(C) Chucky
(D) Dan
(E) Eddie
The following diagram shows a system of balances hanging from the ceiling with three types of weights. The balances tip down to the heavier side. If we use \(\square<\triangle\) to represent \(\square\) is lighter than \(\triangle\), which of the following is true?
(A) \(\square<0<\triangle\)
(B) \(\square<\triangle<0\)
(C) \(\triangle<\square<0\)
(D) \(\triangle<0<\square\)
The integer 6 has exactly four positive factors, namely \(1,2,3\) and \(6\) . Likewise, the integer \(8\) has exactly four positive factors, \(1,2,4\) and \(8\) . How many integers from \(9\) to \(50\) (inclusive) have exactly four positive factors?
(A) \(10\)
(B) \(11\)
(C) \(12\)
(D) \(13\)
(E) \(14\)
A company sells a bottle of juice at \(\$ 1\) per bottle and offers to give you a free bottle of juice if you recycle four empty bottles. Assuming there is no limit to the offer and you can recycle bottles that you receive from the offer, what is the largest number of bottles you can eventually consume if you have \(\$ 43\) ?
(A) 53
(B) 54
(C) 55
(D) 56
(E) 57
Let \(n\) be a positive integer. Suppose the lowest common multiple of \(4,5\) and \(n\) is \(2020\) . What is the sum of the smallest possible value of \(n\) and the largest possible value of \(n\) ?
When the five-digit integer \(\overline{2 x 6 y x}\) is divided by the four-digit integer \(\overline{5 y 27}\), the quotient is 4 and remainder is \(\overline{x 106}\), which is a four-digit integer. What is the value of the digit \(x\) ?
How many multiples of 11 are there in the sequence \(1100,1101,1102, \ldots, 2019,2020\) ?
A quadruple \((a, b, c, d)\) of positive integers is skewed if the median and mode of \(a, b, c, d\) are equal, but strictly greater than the mean of \(a, b, c, d\). How many skewed \((a, b, c, d)\) of positive integers are there that satisfy \(a \leq b \leq c \leq d\) and \(a+b+c+d=40\) ?
Let \(T_n\) be a linear sequence given by
\[
T_1=10, T_2=13, T_3=16, \ldots,
\]
and \(S_n\) be a quadratic sequence given by
\[
S_1=10, S_2=23, S_3=39, \ldots
\]
What is the value of \(S_{101}-T_{101}\) ?
Let \(A B C\) be a triangle where \(D\) is the midpoint of \(B C\) and \(E\) lies on \(A C\) such that \(A E: E C=3: 1\). Let \(F\) be the intersection of \(A D\) and \(B E\). If the area of \(A B C\) is \(280\) , what is the area of triangle \(B F D\) ?
In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If the letter K represents 6 , what number does SHAKE represent?
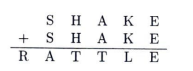
The diagram below shows a shape formed from four semi-circles whose radii are distinct integers. If the shape has perimeter of \(18 \pi\) and encloses an area of \(k \pi\), where \(k\) is a prime, what is the value of \(k\) ?
If the sum of the two diagonals of a kite is \(100\) , what is the largest possible area of the kite?
What is the smallest five-digit integer of the form \(\overline{5 x 20 y}\) that is divisible by \(33\) ?
What is the value of \(2020^3-9(2020)(2017)-2017^3\) ?
In the following diagram, \(A B C D\) is a rectangle where \(E\) and \(F\) are points on \(B C\) and \(C D\) respectively. The area of triangle \(A E F\), denoted \([A E F]\), is \(2037\) . If
\[
[A E C F]=2[A B E]=3[A D F],
\]
what is the area of the rectangle \(A B C D\) ?
In the following diagram, \(A B C D\) is a square of side length \(64\) . \(E\) is the midpoint of \(A B\), \(F\) is the midpoint of \(E C\) and \(G\) is the midpoint of \(F D\). What is the area enclosed by the quadrilateral \(A E F G\) ?
Let \(X=1234 \cdots 78798081\) be the integer that consists of all the integers from \(1\) to \(81\) written from left to right. What is the remainder of \(X\) when divided by \(2020\) ?
Let \(A=\frac{1}{7} \times 3.14 \dot{1} \dot{5}\), where \(3.14 \dot{1} \dot{5}\) is the rational number with recurring digits \(15\) . In other words,
\[
3.14 \dot{1} \dot{5}=3.14+0.0015+0.000015+0.00000015+\cdots \] Suppose that \(A=\frac{m}{n}\), where \(m\) and \(n\) are positive integers with no common factors larger than \(1\) . What is the value of \(m+n\) ?
Ali and Barry went running on a standard \(400\) metre track. They started simultaneously at the same location on the track but ran in opposite directions. Coincidentally, after \(24\) minutes, they ended at the same location where they started. Ali completed \(12\) rounds of the track in those \(24\) minutes while Barry completed \(10\) rounds. How many times did Ali and Barry pass each other during the run? (Exclude from your answer the times that they met at the start of the of run and when they completed the run after \(24\) minutes.)
If we have
\[
(1-3 x)+(1-3 x)^2+\cdots+(1-3 x)^{100}=a_0+a_1 x+a_2 x^2+\cdots+a_{100} x^{100},
\]
for some integers \(a_0, a_1, \ldots, a_{100}\), what is the value of
\[
\left|\frac{a_1}{3}+\frac{a_2}{3^2}+\cdots+\frac{a_{100}}{3^{100}}\right| ?
\]
What is the value of \(\sqrt{27-\sqrt{704}}+\sqrt{27+\sqrt{704}}\) ?
If \(m>n\) are positive integers satisfying
\[
\left(m^2-n^2\right)^2=1+80 n,
\]
what is the smallest possible value of \(mn\) ?
What is the value of
\[\left(\frac{1}{2}+\frac{1}{3}\right+\frac{1}{4}+\frac{1}{5}+\ldots+\frac{1}{37}\right)+\left(\frac{2}{3}+\frac{2}{4}+\frac{2}{5}+\ldots+\frac{2}{37}\right)+\left(\frac{3}{4}+\frac{3}{5}+\frac{3}{6}+\ldots+\frac{3}{37}\right)+\ldots+\left(\frac{35}{36}+\frac{35}{37}\right)+\frac{36}{37}=?\]