Suppose the roots of \(\frac{x^2}{2}+m x+n=0\) are \(\frac{m}{2}\) and \(\frac{n}{3}\). Find the smallest value of \(mn\).
(A) -1080
(B) -90
(C) 0
(D) 90
(E) 1080
Which of the following is true?
(A) \(\sqrt[6]{\frac{1}{333}}<\sqrt[3]{\frac{1}{18}}<\sqrt{\frac{1}{7}}\)
(B) \(\sqrt[3]{\frac{1}{18}}<\sqrt[6]{\frac{1}{333}}<\sqrt{\frac{1}{7}}\)
(C) \(\sqrt[3]{\frac{1}{18}}<\sqrt{\frac{1}{7}}<\sqrt[6]{\frac{1}{333}}\)
(D) \(\sqrt{\frac{1}{7}}<\sqrt[6]{\frac{1}{333}}<\sqrt[3]{\frac{1}{18}}\)
(E) None of the above.
Suppose \(\sqrt{\left(\log {377 \times 377} 2022\right)\left(\log {377} 2022\right)}=\log _k 2022\). Find \(k\).
(A) \(\sqrt{337}\)
(B) \(337^{\sqrt{2}}\)
(C) \(337 \sqrt{2}\)
(D) \(\sqrt{337}^{\sqrt{2}}\)
(E) \(\sqrt{337 \times 2}\)
Suppose \(y=\cos ^2 x-7 \cos x+25\), where \(x\) is any real number. Find the range of \(y\).
(A) \(17 \leq y \leq 33\)
(B) \(18 \leq y \leq 33\)
(C) \(19 \leq y \leq 33\)
(D) \(20 \leq y \leq 33\)
(E) None of the above
Suppose \(\sin \left(180^{\circ}+x\right)=-\frac{7}{9}\), where \(450^{\circ}<x<540^{\circ}\). Find \(\sin (2 x)\).
(A) \(\frac{49}{81} \sqrt{2}\)
(B) \(\frac{56}{81} \sqrt{2}\)
(C) \(-\frac{56}{81}\)
(D) \(-\frac{49}{81} \sqrt{2}\)
(E) \(-\frac{56}{81} \sqrt{2}\)
Find the value of
\(\left(\frac{\cos 10^{\circ}+\cos 50^{\circ}+\cos 70^{\circ}+\cos 110^{\circ}}{\cos 20^{\circ}}\right)^8\) .
Suppose \(x^{20}+\frac{x^{10}}{2}-\frac{3^{2 x}}{9}+\frac{1}{16}=0\) for some positive real number \(x\). Find the value of
\(4 \cdot 3^x-12 x^{10}\).
How many positive integers less than or equal to 2022 cannot be expressed as
\(\lfloor 2 x+1\rfloor+\lfloor 5 x+1\rfloor\) for some real number \(x\) ? Here, \(\lfloor x\rfloor\) denotes the greatest integer less than or equal to \(x\). For example, \(\lfloor-2.1\rfloor=-3,\lfloor 3.9\rfloor=3\).
Suppose
\(y=\frac{\tan ^2 x-\tan x+\sqrt{33}}{\tan ^2 x+\tan x+1}\),
where \(-90^{\circ}<x<90^{\circ}\). Find the maximum possible value of \(\sqrt{33}(y-5)\).
In the figure below, \(P Q R S\) is a square inscribed in a circle. Let \(W\) be a point on the arc \(P Q\) such that \(W S=\sqrt{20}\). Find \((W P+W R)^2\).

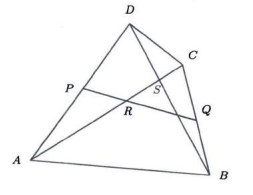
The figure below shows a quadrilateral \(A B C D\) such that \(A C=B D\) and \(P\) and \(Q\) are the midpoints of the sides \(A D\) and \(B C\) respectively. The lines \(P Q\) and \(A C\) meet at \(R\) and the lines \(B D\) and \(A C\) meet at (S). If \(\angle P R C=130^{\circ}\), find the angle \(\angle D S C\) in \({ }^{\circ})\).
How many distinct terms are there if \(\left(x^2+y^2\right)^{11}\left(x^{11}+y^{11}\right)^9\) is algebraically expanded and simplified?
If \(\sqrt{x^2+7 x-4}+\sqrt{x^2-x+4}=x-1\), find the value of \(3 x^2+14 x\).
Let \(k=-1+\sqrt{2022^{1 / 5}-1}\), and let \(f(x)=\left(k^2+2 k+2\right)^{10 x}\). Find the value of \(\log _{2022} f(2022)\).
Find the smallest odd integer \(N\), where \(N>2022\), such that when \(1808,2022\) and \(N\) are each divided by a positive integer \(p\), where \(p>1\), they all leave the same remainder.
If \(\frac{12}{x}+\frac{48}{y}=1\), where \(x\) and \(y\) are positive real numbers, find the smallest possible value of \(x+y\).
Find the largest value of \(40 x+60 y\) if \(x-y \leq 2,5 x+y \geq 5\) and \(5 x+3 y \leq 15\).
Suppose
\(\cos x-\cos y =\frac{1}{2}\),
\(\sin x-\sin y =-\frac{1}{3}\)
If \(\sin (x+y)=\frac{m}{n})\), where \(\frac{m}{n}\) is expressed as a fraction in its lowest terms, find the value of \(m+n\).
For some positive integer \(n\), the number \(n^3-3 n^2+3 n\) has a units digit of \(6\) . Find the product of the last two digits of the number \(7(n-1)^{12}+1\).
Find the largest positive integer \(n\) for which \(\frac{20 n+2020}{3 n-6}\) is a positive integer.
In the \(x y\)-coordinate system, there are two circles passing through the point \(11,3 \sqrt{3}\), and each of these circles is tangent to both the \(x\)-axis and the line \(y=\sqrt{3} x\). Let \(S\) be the sum of the radii of the two circles. Find \(\sqrt{3} S\).
Let \(P\) and \(Q\) be the points \(20(\sqrt{5}-1), 0\) and \(0,10(\sqrt{5}-1)\) on the \(x y\)-plane. Let \(R\) be the point \(a, b\). If \(\angle P R Q\) is a right angle, find the maximum possible value of \(b\).
How many positive integers \(n\) do not satisfy the inequality \(n^{\frac{1}{3} \log _{20} n}>\sqrt{n}\) ?
Let \(f(x)\) be a function such that \(3 f\left(x^2\right)+f(13-4 x)=3 x^2-4 x+293\)
for all real number \(x\). Find the value of \(f(1)\).
Find the largest positive integer \(M\) such that \(\cos ^2 x-\sin ^2 x+\sin x=\frac{M}{888}\) has a real solution.