Try this beautiful problem from the American Invitational Mathematics Examination I, AIME I, 2011 based on Rectangles and sides.
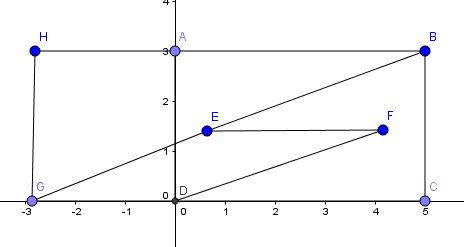
In rectangle ABCD, AB=12 and BC=10 points E and F are inside rectangle ABCD so that BE=9 and DF=8, BE parallel to DF and EF parallel to AB and line BE intersects segment AD. The length EF can be expressed in theorem \(m n^\frac{1}{2}-p\) where m , n and p are positive integers and n is not divisible by the square of any prime, find m+n+p.
Parallelograms
Rectangles
Side Length
Answer: is 36.
AIME I, 2011, Question 2
Geometry Vol I to IV by Hall and Stevens
here extending lines BE and CD meet at point G and drawing altitude GH from point G by line BA extended till H GE=DF=8 GB=17
In a right triangle GHB, GH=10 GB=17 by Pythagorus thorem, HB=(\({{17}^{2}-{10}^{2}})^\frac{1}{2}\)=\(3({21})^\frac{1}{2}\)
HA=EF=\(3({21})^\frac{1}{2}-12\) then 3+21+12=36.
AMC - AIME Boot Camp... for brilliant students.
Use our exclusive one-on-one plus group class system to prepare for Math Olympiad
Publishing original scientific research in a peer-reviewed journal is an achievement many scholars work toward for years. Achieving this feat early in one's academic journey requires exceptional intellectual rigor, creativity, and persistence. Aaditya Punatar and Muskan Sadana have reached this remarkable milestone, successfully publishing their collaborative research paper in the prestigious Journal of Emerging Investigators […]
Her project on quantum-accelerated Steiner trees for 15-minute cities earned a place among the finalists at the world's largest pre-college STEM competition. Prishaa Shrimali of Marymount School of New York, was selected as a Grand Finalist at the 2026 Regeneron International Science and Engineering Fair (ISEF) in Phoenix, Arizona. Her project was Optimizing Urban Accessibility: […]
In 2026, the following Cheenta students have been successful for Indian Statistical Institute's M.Stat Entrance. They ranked within the first 50 in the entire country in these entrances. I.S.I. M.Stat Entrance
In 2026, the following Cheenta students have been successful for Indian Statistical Institute's B.Stat Entrance and Chennai Mathematical Institute's B.Sc. Math Entrance. They ranked within the first 200 in the entire country in these entrances. Most of these students attended the problem solving workshops regularly, which happen 5 days every week. CMI B.Sc. Math Entrance […]