AMERICAN MATHEMATICS COMPETITION 10 A - 2018
Problem 1
What is the value of
$$
\left(\left((2+1)^{-1}+1\right)^{-1}+1\right)^{-1}+1 ?
$$
(A) $\frac{5}{8}$
(B) $\frac{11}{7}$
(C) $\frac{8}{5}$
(D) $\frac{18}{11}$
(E) $\frac{15}{8}$
Answer:
(B) $\frac{11}{7}$
Problem 2
Liliane has $50 \%$ more soda than Jacqueline, and Alice has $25 \%$ more soda than Jacqueline. What is the relationship between the amounts of soda that Liliane and Alica have?
(A) Liliane has $20 \%$ more soda than Alice. (B) Liliane has $25 \%$ more soda than Alice.
(C) Liliane has $45 \%$ more soda than Alice. (D) Liliane has $75 \%$ more soda than Alice.
(E) Liliane has $100 \%$ more soda than Alice.
Answer:
(A) Liliane has $20 \%$ more soda than Alice.
Problem 3
A unit of blood expires after $10!=10 \cdot 9 \cdot 8 \cdots 1$ seconds. Yasin donates a unit of blood at noon of January 1. On what day does his unit of blood expire?
(A) January 2
(B) January 12
(C) January 22
(D) Febuary 11
(E) Febuary 12
Answer:
(E) Febuary 12
Problem 4
How many ways can a student schedule 3 mathematics courses - algebra, geometry, and number theory - in a 6 -period day if no two mathematics courses can be taken in consecutive periods? (What courses the student takes during the other 3 periods is of no concern here.)
(A) 3
(B) 6
(C) 12
(D) 18
(E) 24
Answer:
(E) 24
Problem 5
Alice, Bob, and Charlie were on a hike and were wondering how far away the nearest town was. When Alice said, "We are at least 6 miles away," Bob replied, "We are at most 5 miles away." Charlie then remarked, "Actually the nearest town is at most 4 miles away." It turned out that none of the three statements were true. Let $d$ be the distance in miles to the nearest town. Which of the following intervals is the set of all possible values of $d$ ?
(A) $(0,4)$
(B) $(4,5)$
(C) $(4,6)$
(D) $(5,6)$
(E) $(5, \infty)$
Answer:
(D) $(5,6)$
Problem 6
Sangho uploaded a video to a website where viewers can vote that they like or dislike a video. Each video begins with a score of 0 , and the score increases by 1 for each like vote and decreases by 1 for each dislike vote. At one point Sangho saw that his video had a score of 90 , and that $65 \%$ of the votes cast on his video were like votes. How many votes had been cast on Sangho's video at that point?
(A) 200
(B) 300
(C) 400
(D) 500
(E) 600
Answer:
(B) 300
Problem 7
For how many (not necessarily positive) integer values of $n$ is the value of $4000 \cdot\left(\frac{2}{5}\right)^{n}$ an integer?
(A) 3
(B) 4
(C) 6
(D) 8
(E) 9
Answer:
(E) 9
Problem 8
Joe has a collection of 23 coins, consisting of 5 -cent coins, 10 -cent coins, and 25 -cent coins. He has 3 more 10 -cent coins than 5 -cent coins, and the total value of his collection is 320 cents. How many more 25 -cent coins does Joe have than 5 -cent coins?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Answer:
(C) 2
Problem 9
All of the triangles in the diagram below are similar to iscoceles triangle $A B C$, in which $A B=A C$. Each of the 7 smallest triangles has area 1, and $\triangle A B C$ has area 40 . What is the area of trapezoid $D B C E$ ?
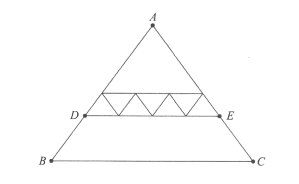
(A) 16
(B) 18
(C) 20
(D) 22
(E) 24
Answer:
(E) 24
Problem 10
Suppose that real number $x$ satisfies
$$
\sqrt{49-x^{2}}-\sqrt{25-x^{2}}=3 .
$$
What is the value of $\sqrt{49-x^{2}}+\sqrt{25-x^{2}}$ ?
(A) 8
(B) $\sqrt{33}+8$
(C) 9
(D) $2 \sqrt{10}+4$
(E) 12
Answer:
(A) 8
Problem 11
When 7 fair standard 6 -sided dice are thrown, the probability that the sum of the numbers on the top faces is 10 can be written as
$$
\frac{n}{6^{7}},
$$
where $n$ is a positive integer. What is $n$ ?
(A) 42
(B) 49
(C) 56
(D) 63
(E) 84
Answer:
(E) 84
Problem 12
How many ordered pairs of real numbers $(x, y)$ satisfy the following system of equations?
$$
\begin{array}{r}
x+3 y=3 \
||x|-|y||=1
\end{array}
$$
(A) 1
(B) 2
(C) 3
(D) 4
(E) 8
Answer:
(C) 3
Problem 13
A paper triangle with sides of lengths 3,4 , and 5 inches, as shown, is folded so that point $A$ falls on point $B$. What is the length in inches of the crease?
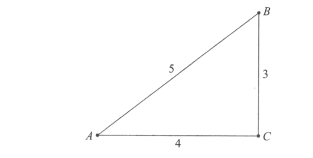
(A) $1+\frac{1}{2} \sqrt{2}$
(B) $\sqrt{3}$
(C) $\frac{7}{4}$
(D) $\frac{15}{8}$
(E) 2
Answer:
(D) $\frac{15}{8}$
Problem 14
What is the greatest integer less than or equal to
$$
\frac{3^{100}+2^{100}}{3^{96}+2^{96}} ?
$$
(A) 80
(B) 81
(C) 96
(D) 97
(E) 625
Answer:
(A) 80
Problem 15
Two circles of radius 5 are externally tangent to each other and are internally tangent to a circle of radius 13 at points $A$ and $B$, as shown in the diagram. The distance $A B$ can be written in the form $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. What is $m+n$ ?
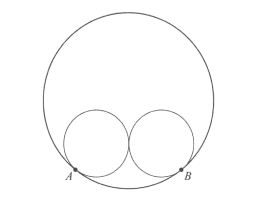
(A) 21
(B) 29
(C) 58
(D) 69
(E) 93
Answer:
(D) 69
Problem 16
Right triangle $A B C$ has leg lengths $A B=20$ and $B C=21$. Including $\overline{A B}$ and $\overline{B C}$, how many line segments with integer length can be drawn from vertex $B$ to a point on hypotenuse $\overline{A C}$ ?
(A) 5
(B) 8
(C) 12
(D) 13
(E) 15
Answer:
(D) 13
Problem 17
Let $S$ be a set of 6 integers taken from ${1,2, \ldots, 12}$ with the property that if $a$ and $b$ are elements of $S$ with $a<b$, then $b$ is not a multiple of $a$. What is the least possible values of an element in $S$ ?
(A) 2
(B) 3
(C) 4
(D) 5
(E) 7
Answer:
(C) 4
Problem 18
How many nonnegative integers can be written in the form
$$
a_{7} \cdot 3^{7}+a_{6} \cdot 3^{6}+a_{5} \cdot 3^{5}+a_{4} \cdot 3^{4}+a_{3} \cdot 3^{3}+a_{2} \cdot 3^{2}+a_{1} \cdot 3^{1}+a_{0} \cdot 3^{0}
$$
where $a_{i} \in{-1,0,1}$ for $0 \leq i \leq 7$ ?
(A) 512
(B) 729
(C) 1094
(D) 3281
(E) 59,048
Answer:
(D) 3281
Problem 19
A number $m$ is randomly selected from the set ${11,13,15,17,19}$, and a number $n$ is randomly selected from ${1999,2000,2001, \ldots, 2018}$. What is the probability that $m^{n}$ has a units digit of 1 ?
(A) $\frac{1}{5}$
(B) $\frac{1}{4}$
(C) $\frac{3}{10}$
(D) $\frac{7}{20}$
(E) $\frac{2}{5}$
Answer:
(E) $\frac{2}{5}$
Problem 20
A scanning code consists of a $7 \times 7$ grid of squares, with some of its squares colored black and the rest colored white. There must be at least one square of each color in this grid of 49 squares. A scanning code is called symmetric if its look does not change when the entire square is rotated by a multiple of $90^{\circ}$ counterclockwise around its center, nor when it is reflected across a line joining opposite corners or a line joining midpoints of opposite sides. What is the total number of possible symmetric scanning codes?
(A) 510
(B) 1022
(C) 8190
(D) 8192
(E) 65,534
Answer:
(B) 1022
Problem 21
Which of the following describes the set of values of $a$ for which the curves $x^{2}+y^{2}=a^{2}$ and $y=x^{2}-a$ in the real $x y$-plane intersect at exactly 3 points?
(A) $a=\frac{1}{4}$
(B) $\frac{1}{4}\frac{1}{4}$
(D) $a=\frac{1}{2}$
(E) $a>\frac{1}{2}$
Answer:
(E) $a>\frac{1}{2}$
Problem 22
Let $a, b, c$, and $d$ be positive integers such that $\operatorname{gcd}(a, b)=24, \operatorname{gcd}(b, c)=36$, $\operatorname{gcd}(c, d)=54$, and $70<\operatorname{gcd}(d, a)<100$. Which of the following must be a divisor of $a$ ?
(A) 5
(B) 7
(C) 11
(D) 13
(E) 17
Answer:
(D) 13
Problem 23
Farmer Pythagoras has a field in the shape of a right triangle. The right triangle's legs have lengths 3 and 4 units. In the corner where those sides meet at a right angle, he leaves a small unplanted square $S$ so that from the air it looks like the right angle symbol. The rest of the fiels is planted. The shortest distance from $S$ to the hypotenuse is 2 units. What fraction of the field is planted?
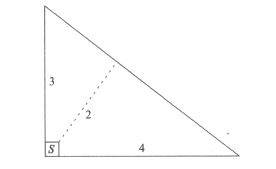
(A) $\frac{25}{27}$
(B) $\frac{26}{27}$
(C) $\frac{73}{75}$
(D) $\frac{145}{147}$
(E) $\frac{74}{75}$
Answer:
(D) $\frac{145}{147}$
Problem 24
Triangle $A B C$ with $A B=50$ and $A C=10$ has area 120 . Let $D$ be the midpoint of $\overline{A B}$, and let $E$ be the midpoint of $\overline{A C}$. The angle bisector of $\angle B A C$ intersects $\overline{D E}$ and $\overline{B C}$ at $F$ and $G$, respectively. What is the area of quadrilateral $F D B G$ ?
(A) 60
(B) 65
(C) 70
(D) 75
(E) 80
Answer:
(D) 75
Problem 25
For a positive integer $n$ and nonzero digits $a, b$, and $c$, let $A_{n}$ be the $n$-digit integer each of whose digits is equal to $a$; let $B_{n}$ be the $n$-digit integer each of whose digits is equal to $b$, and let $C_{n}$ be the $2 n$-digit (not $n$-digit) integer each of whose digits is equal to $c$. What is the greatest possible value of $a+b+c$ for which there are at least two values of $n$ such that $C_{n}-B_{n}=A_{n}^{2}$ ?
(A) 12
(B) 14
(C) 16
(D) 18
(E) 20
Answer:
(D) 18