Author: Kazi Abu Rousan

Where are the zeros of zeta of s?

G.F.B. Riemann has made a good guess;

They're all on the critical line, saith he,

And their density's one over 2 p log t.

Source https://www.physicsforums.com/threads/a-poem-on-the-zeta-function.16280/

If you are a person who loves to read maths related stuff then sure you have came across the words Riemann Zeta function and Riemann Hypothesis at least once. But today we are not going into the Riemann Hypothesis, rather we are going into the Zeta Function. To be more specific, we will see how to calculate the value of zeta function using a simple Julia Program only for $Re(input)>1$.

What is Zeta Function?

What is the Zeta Function?

The Riemann zeta function $\zeta (s)$ is a function of a complex variables $z = \sigma + i t $. When $Re(z) = \sigma >1$, we can define this as a converging summation given by,

$$ \zeta(z) = \sum_{n = 1}^{\infty} \frac{1}{n^z} = \frac{1}{1^z} + \frac{1}{2^z} + \frac{1}{3^z} +\cdots $$

This definition is so simple right?, Here $z$ is a complex number. If it is taken as real, then we will get many famous series like,

Harmonic Series(Diverge as $Re(z)=1$): $H = \zeta(1) = \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots$

Basel problem Series(Converges): $ \zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6}$

and many more.

There are many methods to calculate the values of this function for each value of $n$. You can surely do this by hand although I can't suggest that. The easiest way will be to utilize program.

Code to find the value of zeta for Re(z)>1

Before writing the code, you should remember that the sum is actually infinite. Hence, our function will give us more and more fine result as we include more and more terms.

function ζ(z,limit=1000)
    result = 0
    for i in 1:limit
        result += (1/i)^z
    end
    return result
end

This is the function. How simple!!.. and If we use julia as you can see, we can actually use $\zeta $ symbol. Pretty cool right?

ζ(2,10_0000_000)
#Output: 1.644934057834575
#where pi^2/6 = 1.6449340668482264
#pretty close

It's not all. We can actually apply this function to find the value of zeta function for complex inputs too.

ζ(2+5im)
#Output: 0.8510045028264933 + 0.09880538410302253im

When we use complex inputs, there is a beautiful hidden beauty. Let's see that using a plotting library called Plots and we also have to rewrite our function a little bit.

function ζ(z,limit=1000;point_ar = false)
    points = ComplexF64[0]
    result = 0
    for i in 1:limit
        result += (1/i)^z
        if point_ar
            push!(points,result)
        end
    end
    return result, points
end

Now, we can use this to plot.

z = 2+5im
result, points = ζ(z;point_ar = true)
plot((points),color=:blue,width=3, title="Zeta function spiral",framestyle= :origin,label="$z")
scatter!((points),color=:red, label="Points")S

The output is:

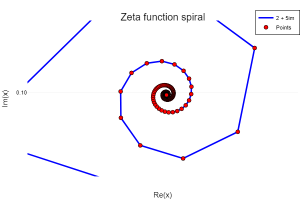
Who would have thought that there will be something like this hidden.

Now, If we apply this function to all possible points of the NumberPlane, then we will get a mesmerizing pattern.

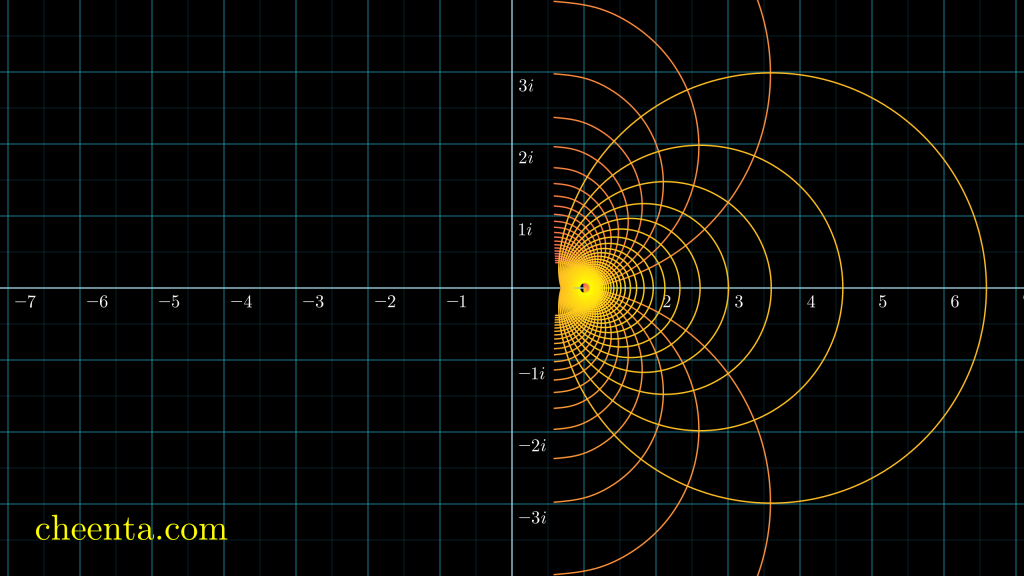
Looking at the image it feels like It's begging to be extended to the other portion. This extension is done using something we called Analytic Continuation. We will not go into much detail here.

If you want to know about the remaining story visit by lecture here:

This is all for today. Why not try to extend the idea to the other side?

Hope you learnt something new.