Cheenta Support
Forum Replies Created
-
Posts
-
Claim : If the entire plane is rotated about any two points, say \(P_1, P_2\) one after the other by angles \(\theta_1, \theta_2\) respectively, then the total transformation of the plane is identical to rotation about some point \(P\) by an angle \(\theta_1+\theta_2\). Here we consider the position of \(P_2\) that do not change upon rotation about \(P_1\).
Proof : Fix the \(X-Y\) coordinate axes and let the coordinates of \(P_1\ ;\ P_2\) be \((x_1, y_1)\ ;\ (x_2,y_2)\) respectively. We represent a point by column matrix and we also know the rotation matrix as defined below. First we shift the axes parallely to \(P_1\) and then rotate by \(\theta_1\) to get the coordinates as,
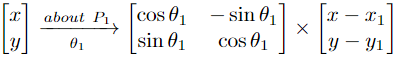
Now, shift the axes parallely to \(P_2\) and then rotate by \(\theta_2\) to get,
and we will finally move the axes back to the actual origin \(O\) (to realize the transformation) which is located at \((-x_2,-y_2)\) with respect to \(P_2\) by subtracting \((-x_2,-y_2)\),
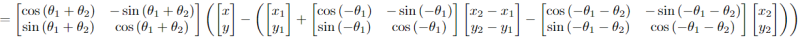
But now observe that this is just rotation by an angle \(\theta_1+\theta_2\) about the point \(P\) given by,
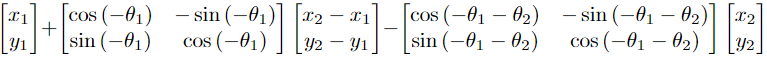
Hence proved the claim \(\blacksquare\).
Now, let us locate the position of point \(P_1=\tau_3\left(\tau_1\left(\tau_2\left(P\right)\right)\right)\). Notice that rotation about point \(A_2\) by \(\angle A_3A_2A_1\) and followed by rotation about point \(A_1\) by \(\angle A_2A_1A_3\) is equivalent to rotation about some point \(Q_1\) by an angle \(\angle A_3A_2A_1+\angle A_2A_1A_3\). Now this followed by a rotation about \(A_3\) by \(\angle A_1A_3A_2\) is totally equivalent to rotation about some point \(R_1\) by angle \(\angle A_3A_2A_1+\angle A_2A_1A_3+\angle A_1A_3A_2\). Note that here the angles are directed module \(360^{\circ}\) and since all these rotation angles have the same orientation (anti-clockwise), they all will have the same sign and add up to give \(180^{\circ}\). So, essentially \(P_1\) is a rotation of \(180^{\circ}\) about some point \(R_1\). Let us now find \(R_1\) by observing the final position of point \(A_2\) upon this transformation.
Let us consider the sides of triangle \(A_2A_3,\ A_3A_1,\ A_1A_2\) to be \(l_1,\ l_2,\ l_3\) respectively as shown. Let \(A_2''=\tau_3\left(\tau_1\left(\tau_2\left(A_2\right)\right)\right)\),
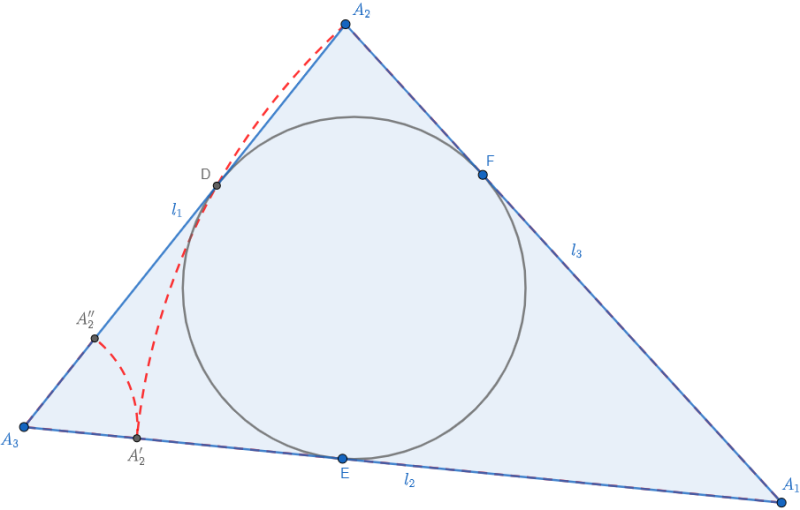
By \(\tau_2,\ A_2\) remains unaltered. Upon applying \(\tau_1,\ A_2\) goes to the point \(A_2'\) such that \(A_3A_2'=l_2-l_3\) (Here the lengths are directed). Now upon applying \(\tau_3,\ A_2'\) goes to \(A_2''\) such that \(A_2A_2''=l_1+l_3-l_2\). So, note that \(A_2''\) is also obtained by rotating about the point \(R_1\) by \(180^{\circ}\), where \(A_2R_1=\frac{l_1+l_3-l_2}{2}\), which is clearly the distance of point of tangency of incircle to the side \(A_2A_3\) from \(A_2\) and hence \(R_1=D\) as shown in the diagram. Also note that this point \(R_1\) is uniquely determined as rotation by \(180^{\circ}\) is nothing but reflection about it. Similarly, \(R_2=E,\ R_3=F\). Hence \(P_1, P_2, P_3\) are obtained by reflection of \(P\) about the points \(D,E,F\) respectively. But, these reflections can be realized as a homothety about \(P\) with scale factor \(2\). Hence, the radius of the circumcircle of \(\triangle P_1P_2P_3\) is \(2r\), where \(r\) denotes the inradius of the \(\triangle A_1A_2A_3\). We also know that \(OI^2=R(R-2r)\), where \(R, O, I\) denote the circumradius, circumcenter, Incenter of the \(\triangle A_1A_2A_3\) respectively. Hence, \[\boxed{Radius\ of\ \Gamma=R\geq 2r= Radius\ of\ circumcircle\ of\ \triangle P_1P_2P_3}\]
Comment out the condition on the \(\triangle A_1A_2A_3\) so that the above inequality turns to equality for any point \(P\) !
Obviously, \(B_n>A_n\ , \forall n\in\mathbb{N}\). Let us bound the value \(B_n-A_n\),
\[B_n-A_n=\left(\sqrt{n^2+2}-\sqrt{n^2+1}\right)+\left(\sqrt{n^2+4}-\sqrt{n^2+3}\right)+\cdots+\left(\sqrt{n^2+2n}-\sqrt{n^2+2n-1}\right)\]
\[=\frac{1}{\sqrt{n^2+2}+\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+4}+\sqrt{n^2+3}}+\cdots+\frac{1}{\sqrt{n^2+2n}+\sqrt{n^2+2n-1}}\]
\[>\frac{1}{\sqrt{n^2+2n}+\sqrt{n^2+2n-1}}+\frac{1}{\sqrt{n^2+2n}+\sqrt{n^2+2n-1}}+\cdots+\frac{1}{\sqrt{n^2+2n}+\sqrt{n^2+2n-1}}\]
\[=\frac{n}{\sqrt{n^2+2n}+\sqrt{n^2+2n-1}}>\frac{n}{\sqrt{n^2+2n+1}+\sqrt{n^2+2n+1}}=\frac{n}{2n+2}\]
Similarly,
\[B_n-A_n<\frac{1}{\sqrt{n^2+2}+\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}+\sqrt{n^2+1}}+\cdots+\frac{1}{\sqrt{n^2+2}+\sqrt{n^2+1}}\]
\[=\frac{n}{\sqrt{n^2+2}+\sqrt{n^2+1}}<\frac{n}{\sqrt{n^2}+\sqrt{n^2}}=\frac{1}{2}\]
Hence, \[\boxed{\frac{n}{2n+2}<B_n-A_n<\frac{1}{2},\ \forall n\in\mathbb{N}}\]
Let \(\{x\}\) denote the fractional part of the real number \(x\) and adding (or) subtracting integer to \(x\) to not alter its fractional part. Then,
\[\{A_n\}=\left\{\left(\sqrt{n^2+1}-n\right)+\left(\sqrt{n^2+3}-n\right)+\cdots+\left(\sqrt{n^2+2n-1}-n\right)\right\}\]
\[\Rightarrow \{A_n\}=\left\{\frac{1}{\sqrt{n^2+1}+n}+\frac{3}{\sqrt{n^2+3}+n}+\cdots+\frac{2n-1}{\sqrt{n^2+2n-1}+n}\right\}\]
Let us now analyse the number \(Y=\frac{1}{\sqrt{n^2+1}+n}+\frac{3}{\sqrt{n^2+3}+n}+\cdots+\frac{2n-1}{\sqrt{n^2+2n-1}+n}\). Note that, \[Y<\frac{1}{\sqrt{n^2+1}+n}+\frac{3}{\sqrt{n^2+1}+n}+\cdots+\frac{2n-1}{\sqrt{n^2+1}+n}\]
\[=\frac{n^2}{\sqrt{n^2+1}+n}<\frac{n^2}{\sqrt{n^2}+n}=\frac{n}{2}\]
Similarly,
\[Y>\frac{1}{\sqrt{n^2+2n-1}+n}+\frac{3}{\sqrt{n^2+2n-1}+n}+\cdots+\frac{2n-1}{\sqrt{n^2+2n-1}+n}\]
\[=\frac{n^2}{\sqrt{n^2+2n-1}+n}>\frac{n^2}{\sqrt{n^2+2n+1}+n}=\frac{n^2}{2n+1}\]
Hence, we get that, \(\frac{n^2}{2n+1}<Y<\frac{n}{2}\). But we have, \(\frac{n^2}{2n+1}>\frac{n-1}{2}>\frac{n}{2}-1\), which is trivial just by cross multiplication. So,
\[\boxed{\frac{n}{2}>Y>\frac{n^2}{2n+1}>\frac{n-1}{2}>\frac{n}{2}-1}\]
Case 1: \(n\) is odd, then \(\{Y\}<\frac{1}{2}\). So, \(\{A_n\}=\{Y\}<\frac{1}{2}\) and hence \(B_n\) and \(A_n\) will have the same integer part since \(B_n-A_n<\frac{1}{2}\)
Case 2: \(n\) is even, then \(\{Y\}>\frac{n^2}{2n+1}-\left(\frac{n}{2}-1\right)=1-\frac{n}{4n+2}>1-\frac{n}{2n+2}\).
Now notice that \(\{A_n\}=\{Y\}>1-\frac{n}{2n+2}\) and we have \(B_n-A_n>\frac{n}{2n+2}\) and adding these both we get \(B_n-(A_n-\{A_n\})>1\Rightarrow B_n-\lfloor A_n\rfloor>1\Rightarrow \lfloor B_n\rfloor\neq \lfloor A_n\rfloor\)
Hence, all the odd numbers \(n\geq 3\) will satisfy \(\lfloor B_n\rfloor=\lfloor A_n\rfloor\) and none of the even numbers satisfy
-
This reply was modified 1 year, 8 months ago by .
-
This reply was modified 1 year, 8 months ago by .
-
This reply was modified 1 year, 8 months ago by .
-
This reply was modified 1 year, 8 months ago by .
-
This reply was modified 1 year, 8 months ago by .
-
This reply was modified 1 year, 8 months ago by .
-
This reply was modified 1 year, 8 months ago by .
-
This reply was modified 1 year, 8 months ago by .
Claim : Mohit can colour a maximum of \(3048000=(2024+1024)\times 1000\) unit squares RED
Proof : First, let us prove that colouring \(3048000\) unit squares is possible. Start by colouring the first consecutive \(1000\) unit squares in each of the \(2024\) rows. Then colour the first \(1000\) unit squares of \(1001^{th}\) column to \(2024^{th}\) column. Now this colouring has \((2024+1024)\times 1000=3048000\) unit squares RED.
Now, let us prove that colouring more than \(3048000\) unit squares RED is impossible. Without loss of generality, we can assume that the initial colouring is done to the first consecutive \(1000\) unit squares in the \(1^{st}\) row. This is because square being symmetric, we may consider column as row by just a rotation and we can rearrange the columns to get the first \(1000\) consecutive squares coloured. Now, none of the first \(1000\) columns can be selected for colouring. So, at most \(2024-1000=1024\) column selections can be done and \(2023\) more row selections can be done as there are only \(2024\) rows in total and we cannot select a row (or) column twice. Hence, at most \((2024+1024)\times 1000=3048000\) unit squares can be coloured RED.
-
This reply was modified 1 year, 8 months ago by