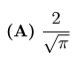American Mathematics Competition 8 - 2026
1 What is the value of the following expression?
1+2-3+4+5-6+7+8-9+10+11-12
A. 18
B. 21
C. 24
D. 27
E. 30
Answer - A
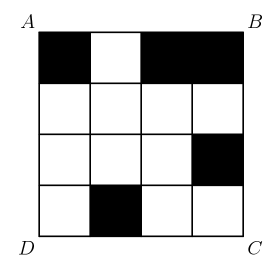
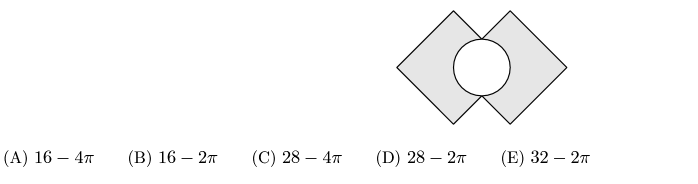
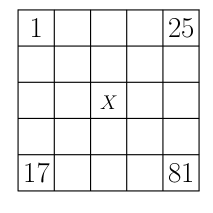
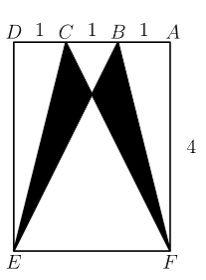
2 In the array shown below, three 3 s are surrounded by 2 s, which are in turn surrounded by a border of 1 s . What is the sum of the numbers in the array?
1 & 1 & 1 & 1 & 1 & 1 & 1
1 & 2 & 2 & 2 & 2 & 2 & 1
1 & 2 & 3 & 3 & 3 & 2 & 1
1 & 2 & 2 & 2 & 2 & 2 & 1
1 & 1 & 1 & 1 & 1 & 1 & 1
A. 49
B. 51
C. 53
D. 55
E. 57
Answer - C
3 Haruki has a piece of wire that is 24 centimeters long. He wants to bend it to form each of the following shapes, one at a time.
A regular hexagon with side length 5 cm .
A square of area $36 \mathrm{~cm}^{2}$.
A right triangle whose legs are 6 and 8 cm long.
Which of the shapes can Haruki make?
A. Triangle only
B. Hexagon and square only
C. Hexagon and triangle only
D. Square and triangle only
E. Hexagon, triangle, and square
Answer - D
4 Brynn's savings decreased by $20 \%$ in July, then increased by $50 \%$ in August. Brynn's savings are now what percent of the original amount?
A. 80
B. 90
C. 100
D. 110
E. 120
Answer - E
5 Casey went on a road trip that covered 100 miles, stopping only for a lunch break along the way. The trip took 3 hours in total and her average speed while driving was 40 miles per hour. In minutes, how long was the lunch break?
A. 15
B. 30
C. 40
D. 45
E. 60
Answer - B
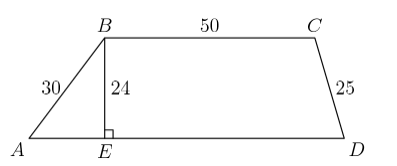
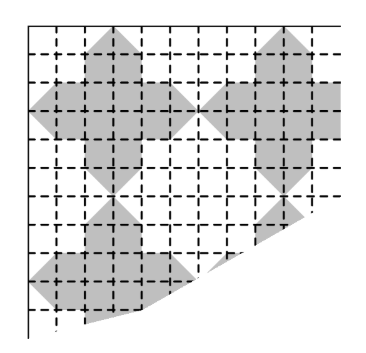
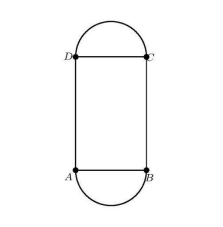
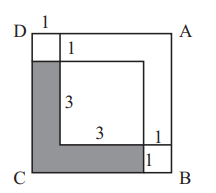
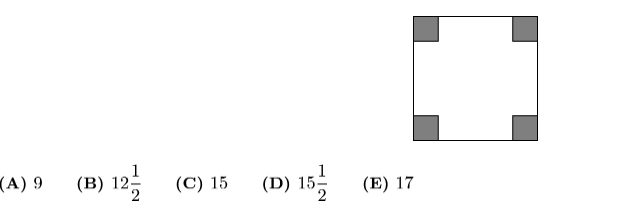
6 Peter lives near a rectangular field that is filled with blackberry bushes. The field is 10 meters long and 8 meters wide, and Peter can reach any blackberries that are within 1 meter of an edge of the field. The portion of the field he can reach is shaded in the figure below. What fraction of the area of the field can Peter reach?
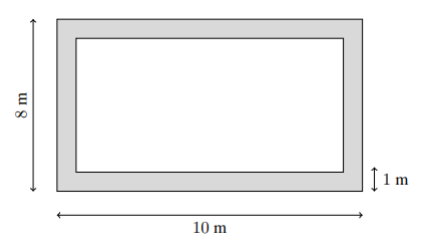
A. $\frac{1}{6}$
B. $\frac{1}{4}$
C. $\frac{1}{3}$
D. $\frac{3}{8}$
E. $\frac{2}{5}$
Answer - E
7 Mika would like to estimate how far she can ride a new model of electric bike on a fully charged battery. She completed two trips totaling 40 miles. The first trip used $\frac{1}{2}$ of the total battery power, while the second trip used $\frac{3}{10}$ of the total battery power. How many miles can this electric bike go on a fully charged battery?
A. 45
B. 48
C. 50
D. 52
E. 55
Answer - C
8. A poll asked a number of people if they liked solving mathematics problems. Exactly $74 \%$ answered "yes." What is the fewest possible number of people who could have been asked the question?
A. 10
B. 20
C. 25
D. 50
E. 100
Answer - D
9 What is the value of this expression?
A. $\frac{4}{9}$
B. $\frac{2}{3}$
C. 1
D. $\frac{3}{2}$
E. $\frac{9}{4}$
Answer - B
10 Five runners completed the grueling Xmarathon: Luke, Melina, Nico, Olympia, and Pedro. Nico finished 11 minutes behind Pedro.
Olympia finished 2 minutes ahead of Melina, but 3 minutes behind Pedro.
Olympia finished 6 minutes ahead of Luke.
Which runner finished fourth?
A. Luke
B. Melina
C. Nico
D. Olympia
E. Pedro
Answer - A
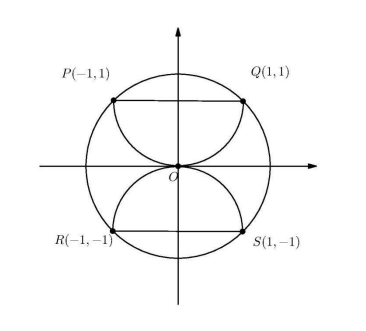
11 Squares of side length $1,1,2,3$, and 5 are arranged to form the rectangle shown below. A curve is drawn by inscribing a quarter circle in each square and joining the quarter circles in order, from shortest to longest. What is the length of the curve?
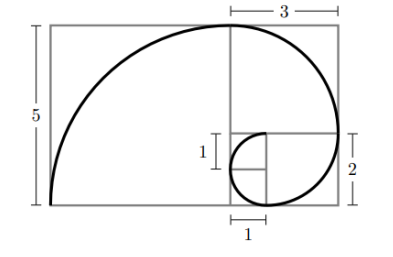
A. $4 \pi$
B. $6 \pi$
C. $\frac{13}{2} \pi$
D. $8 \pi$
E. $13 \pi$
Answer - B
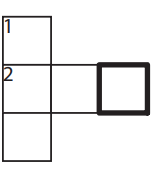
12 In the figure below, each circle will be filled with a digit from 1 to 6 . Each digit must appear exactly once. The sum of the digits in neighboring circles is shown in the box between them. What digit must be placed in the top circle?
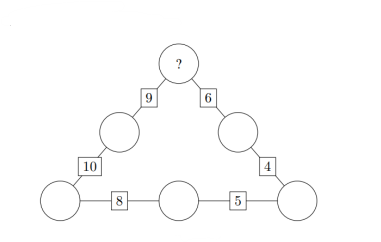
A. 2
B. 3
C. 4
D. 5
E. it is impossible to fill the circles
Answer - D
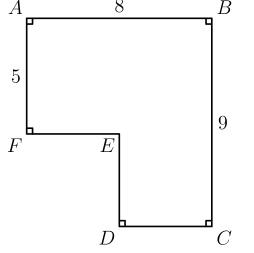
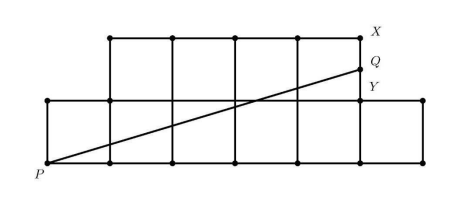
13 The figure below shows a tiling of $1 \times 1$ unit squares. Each row of unit squares is shifted horizontally by half a unit relative to the row above it. A shaded square is drawn on top of the tiling. Each vertex of the shaded square is a vertex of one of the unit squares. In square units, what is the area of the shaded square?
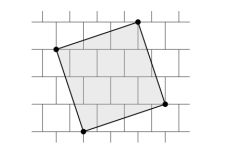
A. 10
B. $\frac{21}{2}$
C. $\frac{32}{3}$
D. 11
E. $\frac{34}{3}$
Answer - A
14 Jami picked three equally spaced integer numbers on the number line. The sum of the first and the second numbers is 40 , while the sum of the second and third numbers is 60 . What is the sum of all three numbers?
A. 70
B. 75
C. 80
D. 85
E. 90
Answer - B
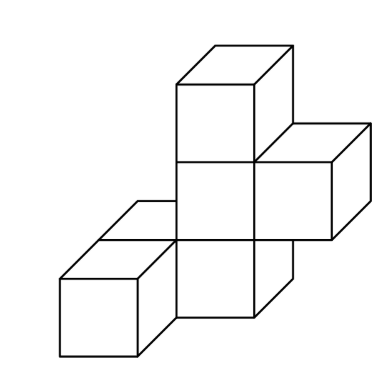
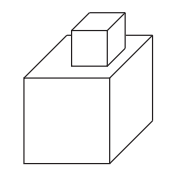
15 Elijah has a large collection of identical wooden cubes which are white on 4 faces and gray on 2 faces that share an edge. He glues some cubes together face-to-face. The figure below shows 2 cubes being glued together, leaving 3 gray faces visible. What is the fewest number of cubes that he could glue together to ensure that no gray faces are visible, no matter how he rotates the figure?
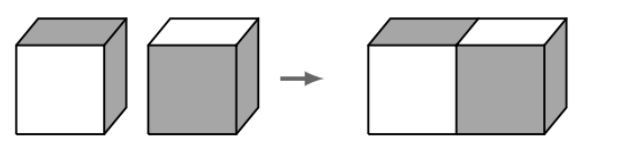
A. 4
B. 6
C. 8
D. 9
E. 27
Answer - A
16 Consider all positive four-digit integers consisting of only even digits. What fraction of these integers are divisible by 4 ?
A. $\frac{1}{4}$
B. $\frac{2}{5}$
C. $\frac{1}{2}$
D. $\frac{3}{5}$
E. $\frac{3}{4}$
Answer - D
17 Four students are seated in a row. They chat with the people sitting next to them, then rearrange themselves so that they are no longer seated next to any of the same people. How many rearrangements are possible?
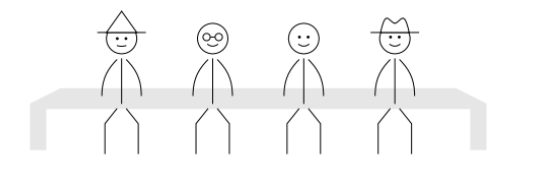
A. 2
B. 4
C. 9
D. 12
E. 24
Answer - A
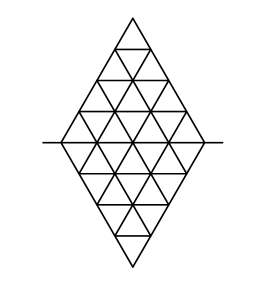
18 In how many ways can 60 be written as the sum of two or more consecutive odd positive integers that are arranged in increasing order?
A. 1
B. 2
C. 3
D. 4
E. 5
Answer - B
19 Miguel is walking with his dog, Luna. When they reach the entrance to a park, Miguel throws a ball straight ahead and continues to walk at a steady pace. Luna sprints toward the ball, which stops by a tree. As soon as the dog reaches the ball, she brings it back to Miguel. Luna runs 5 times faster than Miguel walks. What fraction of the distance between the entrance and the tree does Miguel cover by the time Luna brings him the ball?
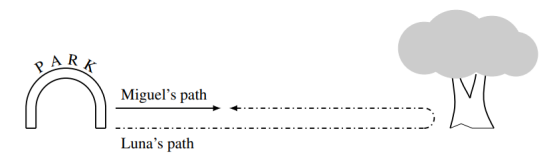
A. $\frac{1}{6}$
B. $\frac{1}{5}$
C. $\frac{1}{4}$
D. $\frac{1}{3}$
E. $\frac{2}{5}$
Answer - D
20 The land of Catania uses gold coins and silver coins. Gold coins are 1 mm thick and silver coins are 3 mm thick. In how many ways can Taylor make a stack of coins that is 8 mm tall using any arrangement of gold and silver coins, assuming order matters?
A. 3
B. 7
C. 10
D. 13
E. 16
Answer - D
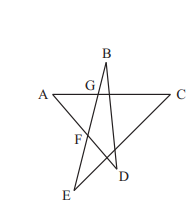
21 Charlotte the spider is walking along a web shaped like a 5 -pointed star, shown in the figure below. The web has 5 outer points and 5 inner points. Each time Charlotte reaches a point, she randomly chooses a neighboring point and moves to that point. Charlotte starts at one of the outer points and makes 3 moves (re-visiting points is allowed). What is the probability she is now at one of the outer points?
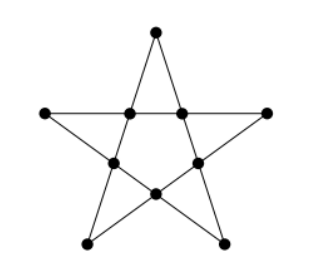
A. $\frac{1}{5}$
B. $\frac{1}{4}$
C. $\frac{2}{5}$
D. $\frac{1}{2}$
E. $\frac{3}{5}$
Answer - B
22 The integers from 1 through 25 are arbitrarily separated into five groups of 5 numbers each. The median of each group is identified. Let $M$ equal the median of the five medians. What is the least possible value of $M$ ?
A. 9
B. 10
C. 12
D. 13
E. 14
Answer - A
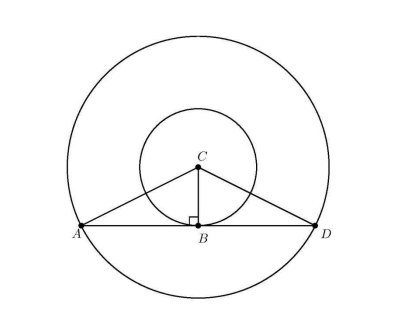
23 Lakshmi has 5 round coins of diameter 4 centimeters. She arranges the coins in 2 rows on a table top, as shown below, and wraps an elastic band tightly around them. In centimeters, what will be the length of the band?
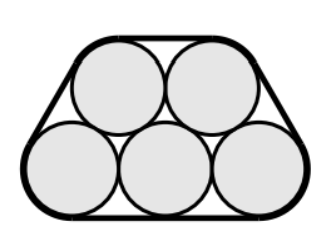
A. $2 \pi+20$
B. $\frac{5}{2} \pi+20$
C. $4 \pi+20$
D. $\frac{9}{2} \pi+20$
E. $5 \pi+20$
Answer - C
24. The notation $n!$ (read " $n$ factorial") is defined as the product of the first $n$ positive integers. (For example, $3!=1 \cdot 2 \cdot 3=6$.) Define the superfactorial of a positive integer, denoted by $n!$, to be the product of the factorials of the first $n$ integers. (For example, $3^{!}=1!\cdot 2!\cdot 3!=12$.) How many factors of 7 appear in the prime factorization of $51^{!}$, the superfactorial of 51 ?
A. 147
B. 150
C. 156
D. 168
E. 171
Answer - E
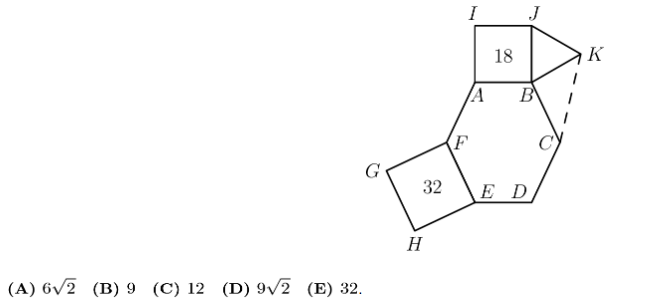
25 In an equiangular hexagon, all interior angles measure $120^{\circ}$. An example of such a hexagon with side lengths of $2,3,1,3,2$, and 2 is shown below, inscribed in equilateral triangle $A B C$. Consider all equiangular hexagons with positive integer side lengths that can be inscribed in $\triangle A B C$, with all six vertices on the sides of the triangle. What is the total number of such hexagons? Hexagons that differ only by a rotation or a reflection are considered the same.
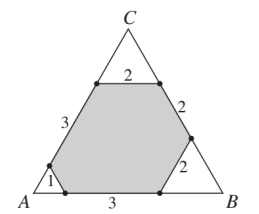
A. 4
B. 5
C. 6
D. 7
E. 8
Answer - E