Announcement of Singapore Mathematical Olympiad:

Schedule of the Test:

Registration Fee:

The registration fee is $8.00 per participant (from SMS institutional member schools) per competition category; and $10.00 per participant (from non-institutional member schools). The participants' names and fees should be forwarded by the Head of the Department of Mathematics (of the competing school) to the Chairman of the Competition Committee in the prescribed format before the announced closing date. Late applications will not be accepted. The receipt of all entries will be acknowledged.

Proving Cyclic Quadrilaterals and Right Angles: A Problem from the Singapore Math Olympiad

In this video, we explore a challenging geometry problem from the Singapore Math Olympiad (Senior Section, Round 2). The problem involves a square, a randomly chosen point on one of its sides, and various perpendiculars and intersections leading to the proof of a right angle. Let’s break down the key concepts used to arrive at the solution.

Problem Overview:

We are given a square $ABCD$ and a point $E$ on side $CD$.
We draw $\triangle AEB$ and drop perpendiculars from points $A$ and $B$ onto the opposite sides $AE$ and $BE$, with the feet of these perpendiculars being points $F$ and $G$, respectively.
We then join $DF$ and $CG$, which intersect at point $H$.
The goal is to prove that the $\angle AHB$ is $90{^\circ}$.

Watch the Video

Key Concepts Used:

Cyclic Quadrilaterals and Concyclic Points: The proof involves showing that multiple points lie on a common circle. The cyclic nature of quadrilaterals helps us determine certain angle relationships that are key to solving the problem.
Angle Chasing: The solution involves a careful examination of angles formed by different line segments and using the properties of cyclic quadrilaterals to establish relationships between them.
Concyclic Conditions: Since points $A$, $F$, $O$, $G$, and $B$ (where $O$ is the center of the square) are concyclic, it follows that the angles subtended by these points must add up to $180{^\circ}$. This property helps prove that $H$ lies on the same circle.

Step-by-Step Proof Summary:

Establish Concyclic Points: We first construct the circumcircle of $\triangle AFB$ and show that it passes through point $G$, making $A$, $F$, $O$, $G$, and $B$ concyclic.
Use Angle Properties: By analyzing the angles subtended by the chords, we establish that the angles at the circumference involving these points are equal, ensuring concyclicity.
Prove Point $H$ Lies on the Circle: By showing that points $F$, $D$, $E$, and $O$ are concyclic, and performing a similar analysis on the other side of the square, we conclude that point $H$ must also lie on the circumcircle.
Conclude with the Right Angle: Since point $H$ lies on the circle whose diameter is segment $AB$, the $\angle AHB$ must be $90{^\circ}$ by the inscribed angle theorem.

This solution beautifully illustrates how advanced geometry concepts like cyclic quadrilaterals, concyclicity, and angle chasing can be used to solve complex problems involving right angles and perpendiculars.

Motivation and Exploration:
The video also discusses the motivation behind defining certain points and relationships, such as the center of the square. Experimentation, including transformations like inversion, can often reveal hidden properties and relationships in geometry. This problem is an excellent example of how problem-solving in geometry is as much about exploration and insight as it is about formal methods.

Singapore Math Olympiad Past Years Questions- Algebra (Senior)

Problem 01: (Year 2023, Problem 01)

Find the value of $m$ such that $2 x^2+3 x+m$ has a minimum value of $9$ .
(A) $\frac{9}{8}$
(B) $-\frac{9}{8}$
(C) $\frac{81}{8}$
(D) $-\frac{81}{8}$
(E) $\frac{63}{8}$

Problem 02: (Year 2023, Problem 03)

If $\log {\sqrt{2}} x=10-3 \log {\sqrt{2}} 10$, find $x$.
(A) 0.32
(B) 0.032
(C) 0.0032
(D) 0.64
(E) 0.064

Problem 03: (Year 2023, Problem 04)

If $(x-5)^2+(y-5)^2=5^2$, find the smallest value of $(x+5)^2+(y+5)^2$.
(A) $225-100 \sqrt{2}$
(B) $225+100 \sqrt{2}$
(C) $225 \sqrt{2}$
(D) $100 \sqrt{2}$
(E) None of the above

Problem 04: (Year 2023, Problem 06)

Suppose the roots of $x^2+11 x+3=0$ are $p$ and $q$, and the roots of $x^2+B x-C=0$ are $p+1$ and $q+1$. Find $C$.

Problem 05: (Year 2023, Problem 07)

If the smallest possible value of $(A-x)(23-x)(A+x)(23+x)$ is $-(48)^2$, find the value of $A$ if $A>0$.

Problem 06: (Year 2023, Problem 12)

Consider the following simultaneous equations:

$ x y^2+x y z=91$
$ x y z-y^2 z=72$,

where $x, y$, and $z$ are positive integers. Find the maximum value of $x z$.

Problem 07: (Year 2023, Problem 14)

A sequence $a_1, a_2, \ldots$, is defined by
$a_1=5, a_2=7, a_{n+1}=\frac{a_n+1}{a_{n-1}} \text { for } n \geq 2$ .
Find the value of $100 \times a_{2023}$

Problem 08: (Year 2023, Problem 15)

Let $C$ be a constant such that the equation $5 \cos x+6 \sin x-C=0$ have two distint roots $a$ and $b$, where $0<b<a<\pi$. Find the value of $61 \times \sin (a+b)$.

Problem 09: (Year 2023, Problem 18)

Let $f(x)=\cos ^2\left(\frac{\pi x}{2}\right)$. Find the value of
$f \left(\frac{1}{2023}\right)+f\left(\frac{2}{2023}\right)+\cdots+f\left(\frac{2021}{2023}\right)+f\left(\frac{2022}{2023}\right)$ .

Problem 10: (Year 2023, Problem 23)

Suppose that there exist numbers $a, b, c$ and a function $f$ such that for any real numbers $x$ and $y$,
$f(x+y)+f(x-y)=2 f(x)+2 f(y)+a x+b y+c$ .
It is given that
$f(2)=3, \quad f(3)=-5, \quad$and $\quad f(5)=7$ . Find the value of $f(123)$.

Problem 11: (Year 2023, Problem 24)

Let $f$ be a function such that for any nonzero number $x$,
$6 x f(x)+5 x^2 f(1 / x)+10=0$ .
Find the value of $f(10)$.

Problem 01: (Year 2022, Problem 01)

Suppose the roots of $\frac{x^2}{2}+m x+n=0$ are $\frac{m}{2}$ and $\frac{n}{3}$. Find the smallest value of $mn$.
(A) -1080
(B) -90
(C) 0
(D) 90
(E) 1080

Problem 07: (Year 2022, Problem 07)

Suppose $x^{20}+\frac{x^{10}}{2}-\frac{3^{2 x}}{9}+\frac{1}{16}=0$ for some positive real number $x$. Find the value of

$4 \cdot 3^x-12 x^{10}$.

Problem 12: (Year 2022, Problem 12)

How many distinct terms are there if $\left(x^2+y^2\right)^{11}\left(x^{11}+y^{11}\right)^9$ is algebraically expanded and simplified?

Problem 13: (Year 2022, Problem 13)

If $\sqrt{x^2+7 x-4}+\sqrt{x^2-x+4}=x-1$, find the value of $3 x^2+14 x$.

Problem 16: (Year 2022, Problem 16)

If $\frac{12}{x}+\frac{48}{y}=1$, where $x$ and $y$ are positive real numbers, find the smallest possible value of $x+y$.

Problem 17: (Year 2022, Problem 17)

Find the largest value of $40 x+60 y$ if $x-y \leq 2,5 x+y \geq 5$ and $5 x+3 y \leq 15$.

Problem 20: (Year 2022, Problem 20)

Find the largest positive integer $n$ for which $\frac{20 n+2020}{3 n-6}$ is a positive integer.

Problem 24: (Year 2022, Problem 24)

Let $f(x)$ be a function such that $3 f\left(x^2\right)+f(13-4 x)=3 x^2-4 x+293$
for all real number $x$. Find the value of $f(1)$.

Problem 01: (Year 2021, Problem 01)

Let $p$ be a real number such that the equation $x^2-10 x=p$ has no real solution. of the following is true?
(A) $0<p<25$
(B) $p = 25$
(C) $p>25$
(D) $p<-25$
(E) $-25<p<0$

Problem 07: (Year 2021, Problem 07)

If $\cos A-\cos B=\frac{1}{2}$ and $\sin A-\sin B=-\frac{1}{4}$, find the value of $100 \sin (A+B)$.

Problem 12: (Year 2021, Problem 12)

Find the sum of all the solutions to the equation $\sqrt[3]{x-110}-\sqrt[3]{x-381}=1$ .

Problem 13: (Year 2021, Problem 13)

If $f(x)=\left(2 x+4+\frac{x-2}{x+3}\right)^2$, where $-2 \leq x \leq 2$, find the maximum value of $f(x)$.

Problem 14: (Year 2021, Problem 14)

Given that $D=\sqrt{\sqrt{x^2+(y-1)^2}+\sqrt{(x-1)^2+y^2}}$ for real values of (x) and (y), find the minimum value of $D^8$.

Problem 18: (Year 2021, Problem 18)

A function $f$ satisfies $f(x) f(x+1)=x^2+3 x$ for all real numbers $x$. If $f(1)+f(2)=\frac{25}{6}) and (0<f(1)<2$, determine the value of $11 \times f(10)$.

Problem 20: (Year 2021, Problem 20)

Let $a_1, a_2, a_3$ be three distinct integers where $1000>a_1>a_2>a_3>0$. Suppose there exist real numbers $x, y, z$ such that
$\left(a_1-a_2\right) y+\left(a_1-a_3\right) z=a_1+a_2+a_3 $
$ \left(a_1-a_2\right) x+\left(a_2-a_3\right) z=a_1+a_2+a_3 $
$\left(a_1-a_3\right) x+\left(a_2-a_3\right) y=a_1+a_2+a_3$ .

Find the largest possible value of $x+y+z$.

Problem 22: (Year 2021, Problem 22)

Find the number of real solutions $x, y$ of the system of equations

$x^3+y^3+y^2 =0, $
$x^2+x^2 y+x y^2 =0$ .

Problem 24: (Year 2021, Problem 24)

Let $n$ be a positive integer such that $\frac{2021 n}{2021+n}$ is also a positive integer. Determine the smallest possible value of (n).

Problem 25: (Year 2020, Problem 01)

Let $b$ be a positive integer. If the minimum possible value of the quadratic function $5 x^2+b x+506$ is $6$ , find the value of $b$.
(A) 90
(B) 100
(C) 110
(D) 120
(E) 130

Problem 26: (Year 2020, Problem 05)

Let $p=\log _{10}(\sin x), q=(\sin x)^{10}, r=10^{\sin x}$, where $0<x<\frac{\pi}{2}$. Which of the following is true? following is true?
(A) $p<q<r$
(B) $p<r<q$
(C) $q<r<p$
(D) $q<p<r$
(E) $r<p<q$

Problem 27: (Year 2020, Problem 10)

Find the number of ordered pairs $x, y$, where $x$ and $y$ are integers, such that
$x^2+y^2-20 x-14 y+140<0$ .

Problem 28: (Year 2020, Problem 14)

If $\frac{x^2}{5}+\frac{y^2}{7}=1$, find the largest possible value of $(x+y)^2$.

Problem 29: (Year 2020, Problem 15)

Find the coefficient of $x^6$ in the expansion of $\left(1+x+2 x^2\right)^7$.

Problem 30: (Year 2020, Problem 16)

Suppose $3 x-y)^2+\sqrt{x+38+14 \sqrt{x-11}}+|z+x-y|=7$. Find the value of $|x+y+z|$.

Problem 31: (Year 2020, Problem 17)

Suppose there are real numbers (x, y, z) satisfying the following equations: $x+y+z=60, x y-z^2=900$ Find the maximum possible value of $|z|$.

Problem 32: (Year 2020, Problem 18)

Find the sum $\sum_{k=1}^{16} \log _2\left(\sqrt{\sin ^2 \frac{k \pi}{8}+1}-\sin \frac{k \pi}{8}\right)$

Problem 33: (Year 2019, Problem 01)

The roots of the quadratic equation $x^2-7 m x+5 n=0$ are $m$ and $n$, where $m \neq 0$ and $n \neq 0$. Find a quadratic equation whose roots are $\frac{m}{n}$ and $\frac{n}{m}$.
(A) $6 x^2-37 x+1=0$
(B) $6 x^2-50 x-7=0$
(C) $6 x^2-50 x+7=0$
(D) $6 x^2-37 x+6=0$
(E) $x^2-37 x+1=0$

Problem 34: (Year 2019, Problem 08)

Suppose (x) and (y) are real numbers such that
\[
|x-y|+3 x-y=70, \text { and } \
|y-x|+3 y+x=50 .
\]

Problem 35: (Year 2019, Problem 13)

Let $P(x)$ be the polynomial that results from the expansion of the following expression:
\[
\left(2 x^3+3 x^2+x\right)^5\left(\frac{x}{6}+\frac{1}{2}\right)^5 .
\]

Find the sum of the coefficients of $x^{2 k+1}$, where $k=0,1,2,3, \ldots, 9$.

Problem 36: (Year 2019, Problem 15)

Let $M$ be the maximum possible value of $\frac{15 x^2-x^3-39 x-54}{x+1}$, where $x$ is a positive integer. Find the value of $9 M$.

Problem 37: (Year 2019, Problem 16)

Find the maximum possible value of $x+y+z$ where $x, y, z$ are integers satisfying the following system of equations:
\[
x^2 z+y^2 z+8 x y=200 \
2 x^2+2 y^2+x y z=50 .
\]

Problem 38: (Year 2019, Problem 18)

Suppose $\left(\log _2 x\right)^2$+$4\left(\log _2\left(\log _3 y\right)\right)^2$ = $4\left(\log _2 x\right)\left(\log _2\left(\log _3 y\right)\right)$. If $x = 49$ and $y$ is a positive integer, find $y$.

Problem 39: (Year 2019, Problem 20)

A sequence $x_0, x_1, x_2, x_3, \ldots$ of integers satisfies the following conditions: $x_0=1$, and for any positive integer $n \geq 1,\left|x_n-1\right|=\left|x_{n-1}+2\right|$. Find the maximum possible value of $2019-\left(x_1+x_2+\cdots+x_{2018}\right)$.

Problem 40: (Year 2019, Problem 23)

Let $k$ be a positive integer and let the function $f$ be defined as follows:
\[
f(x)=\frac{\pi^x}{\pi^x+\pi^{2 k-x}} .
\]

Suppose the function $g(k)$ is defined as follows:
\[
g(k)=f(0)+f\left(\frac{k}{2019}\right)+f\left(\frac{2 k}{2019}\right)+f\left(\frac{3 k}{2019}\right)+\ldots+f\left(\frac{4037 k}{2019}\right)+f(2 k) .
\]

Find the greatest positive integer $n$ such that $g(k) \geq n$ for all $k \geq 1$.

Problem 41: (Year 2019, Problem 25)

Suppose (a) and (b) are positive integers satisfying
$a^2-2 b^2=1$ .

If $500<a+b<1000$, find $a+b$.

Singapore Math Olympiad Past Years Questions- Number Theory (Senior)

Problem 01: (Year 2023, Problem 04)

If $\log {\sqrt{2}} x=10-3 \log {\sqrt{2}} 10$, find $x$.
(A) 0.32
(B) 0.032
(C) 0.0032
(D) 0.64
(E) 0.064

Problem 02: (Year 2023, Problem 08)

Find the smallest positive odd integer greater than 1 that is a factor of
$(2023)^{2023}+(2026)^{2026}+(2029)^{2029}$ .

Problem 03: (Year 2023, Problem 09)

Find the remainder of $7^{2023}+9^{2023}$ when divided by $64$ .

Problem 04: (Year 2023, Problem 10)

Let $x, y, z>1$, and let $A$ be a positive number such that $\log x A=30, \log _y A=50$ and $\log {x y}(A z)=150$. Find

$\left(\log _A z\right)^2$.

Problem 05: (Year 2023, Problem 11)

Find the largest integer that is less than
$\text { - } \frac{3^{10}-2^{10}}{10 !}\left(\frac{1}{1 ! 9 ! 2}+\frac{1}{2 ! 8 ! 2^2}+\frac{1}{3 ! 7 ! 2^3}+\cdots+\frac{1}{9 ! 1 ! 2^9}\right)^{-1}$ .

Here, $n !=n \cdot(n-1) \cdots 3 \cdot 2 \cdot 1$. For example, $5 !=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120$.

Problem 06: (Year 2023, Problem 19)

Find the remainder when $3^{2023}$ is divided by $215$ .

Problem 07: (Year 2023, Problem 20)

Find the sum of the prime divisors of $64000027$ .

Problem 08: (Year 2022, Problem 02)

Which of the following is true?
(A) $\sqrt[6]{\frac{1}{333}}<\sqrt[3]{\frac{1}{18}}<\sqrt{\frac{1}{7}}$
(B) $\sqrt[3]{\frac{1}{18}}<\sqrt[6]{\frac{1}{333}}<\sqrt{\frac{1}{7}}$
(C) $\sqrt[3]{\frac{1}{18}}<\sqrt{\frac{1}{7}}<\sqrt[6]{\frac{1}{333}}$
(D) $\sqrt{\frac{1}{7}}<\sqrt[6]{\frac{1}{333}}<\sqrt[3]{\frac{1}{18}}$
(E) None of the above.

Problem 09: (Year 2022, Problem 03)

Suppose $\sqrt{\left(\log {377 \times 377} 2022\right)\left(\log {377} 2022\right)}=\log _k 2022$. Find $k$.
(A) $\sqrt{337}$
(B) $337^{\sqrt{2}}$
(C) $337 \sqrt{2}$
(D) $\sqrt{337}^{\sqrt{2}}$
(E) $\sqrt{337 \times 2}$

Problem 10: (Year 2022, Problem 08)

How many positive integers less than or equal to 2022 cannot be expressed as
$\lfloor 2 x+1\rfloor+\lfloor 5 x+1\rfloor$ for some real number $x$ ? Here, $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$. For example, $\lfloor-2.1\rfloor=-3,\lfloor 3.9\rfloor=3$.

Problem 11: (Year 2022, Problem 14)

Let $k=-1+\sqrt{2022^{1 / 5}-1}$, and let $f(x)=\left(k^2+2 k+2\right)^{10 x}$. Find the value of $\log _{2022} f(2022)$.

Problem 12: (Year 2022, Problem 15)

Find the smallest odd integer $N$, where $N>2022$, such that when $1808,2022$ and $N$ are each divided by a positive integer $p$, where $p>1$, they all leave the same remainder.

Problem 13: (Year 2022, Problem 19)

For some positive integer $n$, the number $n^3-3 n^2+3 n$ has a units digit of $6$ . Find the product of the last two digits of the number $7(n-1)^{12}+1$.

Problem 14: (Year 2022, Problem 23)

How many positive integers $n$ do not satisfy the inequality $n^{\frac{1}{3} \log _{20} n}>\sqrt{n}$ ?

Problem 15: (Year 2021, Problem 03)

Find the value of $2021^{\left(\log {2021} 2020\right)\left(\log {2020} 2019\right)\left(\log _{2019} 2018\right)}$.
(A) 2018
(B) 2019
(C) 2020
(D) 2021
(E) None of the above

Problem 16: (Year 2021, Problem 05)

Select all the inequalities which hold for all real values of (x) and (y).

(i) $x \leq x^2+y^2$,
(ii) $x y \leq x^2+y^2$,
(iii) $x-y \leq x^2+y^2$,
(iv) $y+x y \leq x^2+y^2$,
(v) $x+y-1 \leq x^2+y^2 $.
(A) (i)
(B) (i) and (iii)
(C) (iii) and (iv)
(D) (ii)
(E) (ii) and (v)

Problem 17: (Year 2021, Problem 06)

Let $x$ be the integer such that $x=5 \sqrt{2+4 \log _x 5}$. Determine the value of $x$.

Problem 18: (Year 2021, Problem 24)

Let $n$ be a positive integer such that $\frac{2021 n}{2021+n}$ is also a positive integer. Determine the smallest possible value of (n).

Problem 19: (Year 2021, Problem 25)

Determine the number of 5-digit numbers with the following properties:
(i) All the digits are non-zero;
(ii) The digits can be repeated;
(iii) The difference between consecutive digits is exactly 1 .

Problem 20: (Year 2020, Problem 02)

Which of the following is equal to $\sqrt{5+\sqrt{3}}+\sqrt{5-\sqrt{3}}$ ?
(A) $\sqrt{10-\sqrt{22}}$
(B) $\sqrt{10+\sqrt{22}}$
(C) $\sqrt{10-2 \sqrt{22}}$
(D) $\sqrt{10+2 \sqrt{22}}$
(E) None of the above

Problem 21: (Year 2020, Problem 03)

Simplify
$\log 8 5 \cdot\left(\log _5 3+\log {25} 9+\log _{125} 27\right)$ .
(A) $\log _2 3$
(B)$\log _3 2$
(C) $\log _2 9$
(D) $\log _3 16$
(E) $\log _2 27$

Problem 22: (Year 2020, Problem 04)

Let $a=50^{\frac{1}{505}}, b=10^{\frac{1}{303}}$ and $c=6^{\frac{1}{202}}$. Which of the following is true?
(A) $a<b<c$
(B) $a<c<b$
(C) $b<a<c$
(D) $b<c<a$
(E) $c<b<a$

Problem 23: (Year 2020, Problem 06)

Find the minimum possible value of $|x-10|-|x-20|+|x-30|$, where $x$ is any real number.

Problem 24: (Year 2020, Problem 19)

Let $a, b$ be positive real numbers, where $a>b$. Suppose there exists a real number (x) such that $\left(\log _2 a x\right)\left(\log _2 b x\right)+25=0$. Find the minimum possible value of $\frac{a}{b}$.

Problem 25: (Year 2020, Problem 21)

Find the smallest positive integer that is greater than the following expression:
($\sqrt{7}+\sqrt{5})^4$.

Problem 26: (Year 2020, Problem 24)

The digit sum of a number, say 987 , is the sum of its digits, $9+8+7=24$. Let (A) be the digit sum of $2020^{2021}$, and let (B) be the digit sum of (A). Find the digit sum of (B).

Problem 27: (Year 2020, Problem 25)

$40=2 \times 2 \times 2 \times 5$ is a positive divisor of 1440 that is a product of 4 prime numbers. $48=2 \times 2 \times 2 \times 2 \times 3$ is a positive divisor of 1440 that is a product of 5 prime numbers. Find the sum of all the positive divisors of 1440 that are products of an odd number of prime numbers.

Problem 28: (Year 2019, Problem 02)

Simplify
\[
(\sqrt{10}-\sqrt{2})^{\frac{1}{3}}(\sqrt{10}+\sqrt{2})^{\frac{7}{3}} .
\]
(A) $24+4 \sqrt{5}$
(B) $24+6 \sqrt{5}$
(C) $24+8 \sqrt{5}$
(D) $24+10 \sqrt{5}$
(E) $24+12 \sqrt{5}$

Problem 29: (Year 2019, Problem 03)

Let $a=4^{3000}, b=6^{2500}$ and $c=7^{2000}$. Which of the following statement is true?
(A) $a<b<c$
(B) $a<c<b$
(C) $b<a<c$
(D) $c<a<b$
(E) $c<b<a$

Problem 30: (Year 2019, Problem 04)

If $\log _{21} 3=x$, express $\log _7 9$ in terms of $x$.
(A) $\frac{2 x}{2-x}$
(B) $\frac{2 x}{1-x}$
(C) $\frac{2 x}{x-2}$
(D) $\frac{2 x}{x-1}$
(E) $\frac{x}{1-x}$

Problem 31: (Year 2019, Problem 06)

Find the largest positive integer (n) such that (n+8) is a factor of $n^3+13 n^2+40 n+40$.

Problem 32: (Year 2019, Problem 14)

Find the value of the following expression:
\[
\frac{2\left(1^2+2^2+3^2+\ldots+49^2+50^2\right)+(1 \times 2)+(2 \times 3)+(3 \times 4)+\ldots+(48 \times 49)+(49 \times 50)}{100} .
\]

Problem 33: (Year 2019, Problem 17)

Find the remainder when $10^{43}$ is divided by $126$ .

Singapore Math Olympiad Past Years Questions- Geometry (Senior)

Problem 01: (Year 2023, Problem 02)

Which of the following is true?
(A) $\sin \left(105^{\circ}\right)-\cos \left(105^{\circ}\right)=\frac{\sqrt{3}}{2}$
(B) $\sin \left(105^{\circ}\right)-\cos \left(105^{\circ}\right)=\frac{\sqrt{3}}{\sqrt{2}}$
(C) $\sin \left(105^{\circ}\right)+\cos \left(105^{\circ}\right)=\frac{1}{2}$
(D) $\sin \left(105^{\circ}\right)+\cos \left(105^{\circ}\right)=\frac{1}{\sqrt{3}}$
(E) None of the above.

Problem 02: (Year 2023, Problem 05)

Suppose $\cos \left(180^{\circ}+x\right)=\frac{4}{5}$, where $90^{\circ}<x<180^{\circ}$. Find $\tan (2 x)$.

(A) $\frac{24}{7}$
(B) $\frac{7}{24}$
(C) $-\frac{24}{7}$
(D) $-\frac{7}{24}$
(E) $-\frac{24}{25}$

Problem 03: (Year 2023, Problem 13)

Let $x$ be a real number such that
$\frac{\sin ^4 x+\cos ^4 x}{\sin ^2 x+\cos ^4 x}=\frac{8}{11}$ .
Assuming $\sin ^2 x>\frac{1}{2}$, find the value of $\sqrt{28}\left(\sin ^4 x-\cos ^4 x\right)$.

Problem 04: (Year 2023, Problem 15)

Let $C$ be a constant such that the equation $5 \cos x+6 \sin x-C=0$ have two distint roots $a$ and $b$, where $0<b<a<\pi$. Find the value of $61 \times \sin (a+b)$.

Problem 05: (Year 2023,Problem 16)

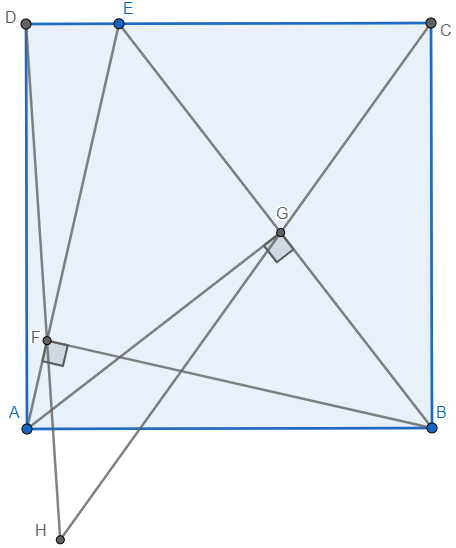
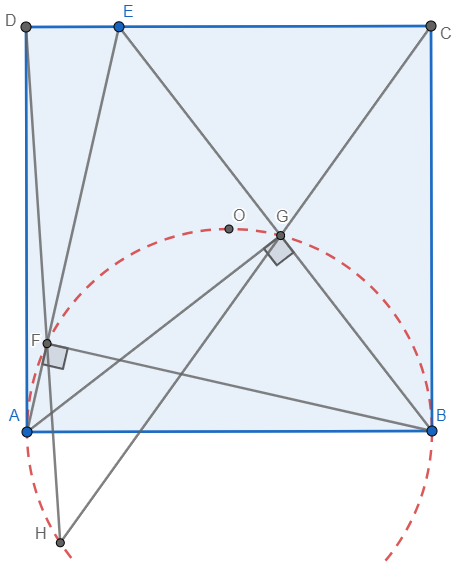
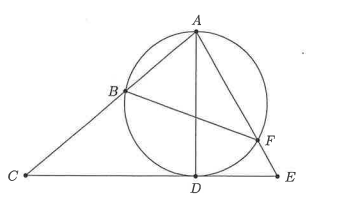
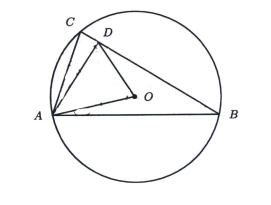
In the diagram below, $C E$ is tangent to the circle at point $D, A D$ is a diameter of the circle, and $A B C, A F E$ are straight lines. It is given that $\frac{A B}{A C}=\frac{16}{41}$ and $\frac{A F}{A E}=\frac{49}{74}$. Let $\tan (\angle C A E)=\frac{m}{n}$, where $m, n$ are positive integers and $\frac{m}{n}$ is a fraction in its lowest form. Find the sum $m+n$.

Problem 06: (Year 2023, Problem 18)

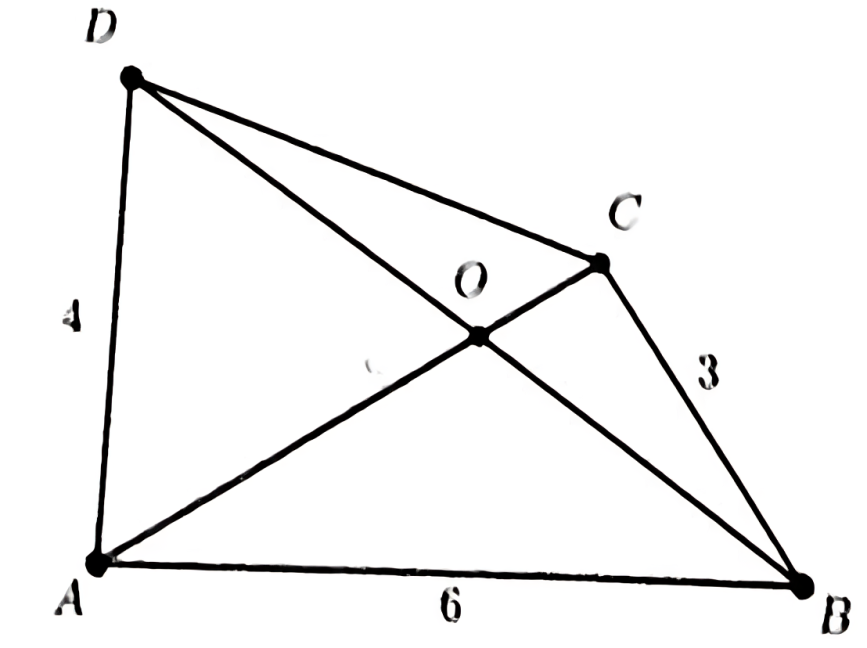
Problem 07: (Year 2023,Problem 17)

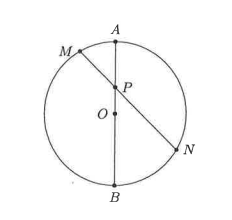
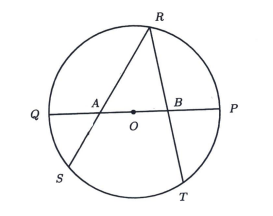
In the diagram below, $A B$ is a diameter of the circle with centre $O, M N$ is a chord of the circle that intersects $A B$ at $P, \angle B O N$ and $\angle M O A$ are acute angles, $\angle M P A=45^{\circ}$, $M P=\sqrt{56}$, and $N P=12$. Find the radius of the circle.

Problem 08:(Year 2023, Problem 23)

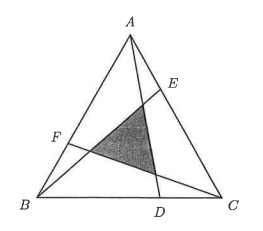
Let $\triangle A B C$ be an equilateral triangle. $D, E, F$ are points on the sides such that
$B D: D C=C E: E A=A F: F B=2: 1$ .
Suppose the area of the triangle bounded by $A D, B E$ and $C F$ is $2023$ . Find the area of $\triangle A B C$.

Problem 09: (Year 2023, Problem 25)

Find the number of triangles such that all the sides are integers and the area equals the perimeter (in number).

Problem 10: (Year 2022, Problem 04)

Suppose $y=\cos ^2 x-7 \cos x+25$, where $x$ is any real number. Find the range of $y$.
(A) $17 \leq y \leq 33$
(B) $18 \leq y \leq 33$
(C) $19 \leq y \leq 33$
(D) $20 \leq y \leq 33$
(E) None of the above

Problem 11: (Year 2022, Problem 05)

Suppose $\sin \left(180^{\circ}+x\right)=-\frac{7}{9}$, where $450^{\circ}<x<540^{\circ}$. Find $\sin (2 x)$.
(A) $\frac{49}{81} \sqrt{2}$
(B) $\frac{56}{81} \sqrt{2}$
(C) $-\frac{56}{81}$
(D) $-\frac{49}{81} \sqrt{2}$
(E) $-\frac{56}{81} \sqrt{2}$

Problem 12: (Year 2022, Problem 06)

Find the value of
$\left(\frac{\cos 10^{\circ}+\cos 50^{\circ}+\cos 70^{\circ}+\cos 110^{\circ}}{\cos 20^{\circ}}\right)^8$ .

Problem 13: (Year 2022, Problem 09)

Suppose
$y=\frac{\tan ^2 x-\tan x+\sqrt{33}}{\tan ^2 x+\tan x+1}$,
where $-90^{\circ}<x<90^{\circ}$. Find the maximum possible value of $\sqrt{33}(y-5)$.

Problem 14: (Year 2022,Problem 10)

In the figure below, $P Q R S$ is a square inscribed in a circle. Let $W$ be a point on the arc $P Q$ such that $W S=\sqrt{20}$. Find $(W P+W R)^2$.

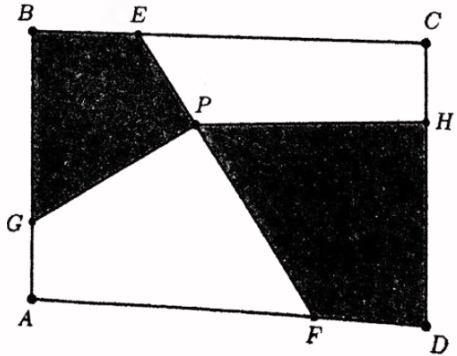
Problem 15: (Year 2022, Problem 11)

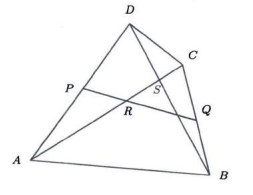
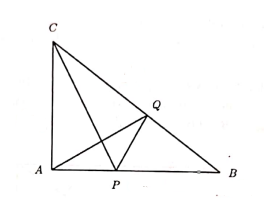
The figure below shows a quadrilateral $A B C D$ such that $A C=B D$ and $P$ and $Q$ are the midpoints of the sides $A D$ and $B C$ respectively. The lines $P Q$ and $A C$ meet at $R$ and the lines $B D$ and $A C$ meet at (S). If $\angle P R C=130^{\circ}$, find the angle $\angle D S C$ in ${ }^{\circ})$.

Problem 16: (Year 2022, Problem 18)

Suppose
$\cos x-\cos y =\frac{1}{2}$,
$\sin x-\sin y =-\frac{1}{3}$

If $\sin (x+y)=\frac{m}{n})$, where $\frac{m}{n}$ is expressed as a fraction in its lowest terms, find the value of $m+n$.

Problem 17: (Year 2022, Problem 25)

Find the largest positive integer $M$ such that $\cos ^2 x-\sin ^2 x+\sin x=\frac{M}{888}$ has a real solution.

Problem 18: (Year 2021, Problem 02)

Which of the following is the largest?
(A) $\tan 50^{\circ}+\sin 50^{\circ}$
(B) $\tan 50^{\circ}+\cos 50^{\circ}$
(C) $\sin 50^{\circ}+\cos 50^{\circ}$
(D) $\tan 50^{\circ}+\sin ^2 50^{\circ}$
(E) $\sin ^2 50^{\circ}+\cos ^2 50^{\circ}$

Problem 19: (Year 2021, Problem 04)

Suppose $\sin \theta=\frac{n-3}{n+5}$ and $\cos \theta=\frac{4-2 n}{n+5}$ for some integer $n$. Find the maximum value of $160 \tan ^2 \theta$.
(A) 80
(B) 90
(C) 100
(D) 120
(E) None of the above

Problem 20: (Year 2021, Problem 07)

If $\cos A-\cos B=\frac{1}{2}$ and $\sin A-\sin B=-\frac{1}{4}$, find the value of $100 \sin (A+B)$.

Problem 21:(Year 2021, Problem 10)

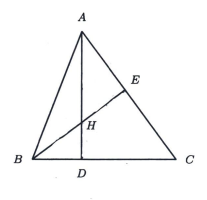
The figure below shows a triangle $A B C$ such that $A D$ and $B E$ are altitudes to the sides $B C$ and $C A$ respectively. The lines $A D$ and $B E$ intersect at $H$. Determine the area in $\mathrm{cm}^2$ of the triangle $A B C$ if $A H=50 \mathrm{~cm}, D H=18 \mathrm{~cm}$ and $B H=E H$.

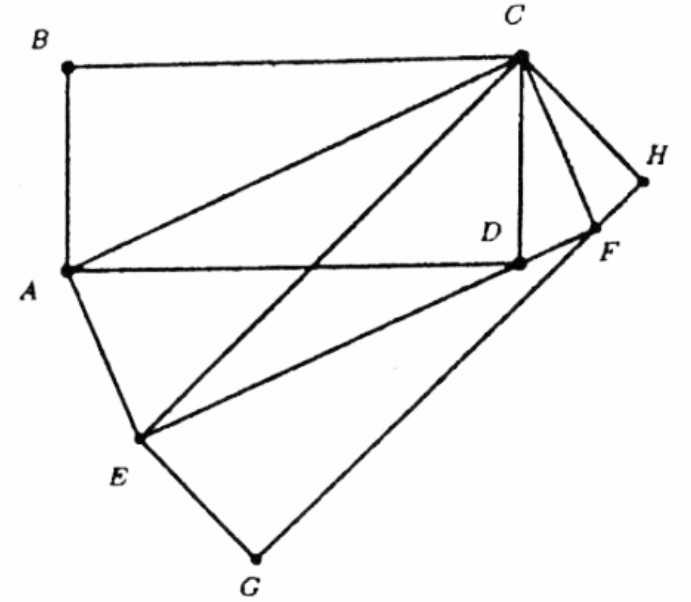
Problem 22:(Year 2021, Problem 12)

In the figure below, $\angle G C B=\angle A C E=\angle D F E=90^{\circ}$, and $\angle G B C=\angle E A C=$ $\angle E D F=\theta^{\circ}$. Also, $G B=6 \mathrm{~cm}, A E=10 \mathrm{~cm}$ and $D E=8 \mathrm{~cm}$. Let $\mathcal{S}$ denote the sum of the areas of the triangles $A B C$ and $C D E$. Find the maximum possible value of $\mathcal{S}$ in $\mathrm{cm}^2$ .

Problem 23: (Year 2021, Problem 15)

Find the minimum value of $\frac{8}{\sin 2 \theta}+12 \tan \theta$, where $0<\theta<\frac{\pi}{2}$.

Problem 24: (Year 2021, Problem 16)

Determine the largest angle $\theta$ (in degree), where $0^{\circ} \leq \theta \leq 360^{\circ}$, such that $\sin \left(\theta+18^{\circ}\right)+\sin \left(\theta+162^{\circ}\right)+\sin \left(\theta+234^{\circ}\right)+\sin \left(\theta+306^{\circ}\right)=1+\cos \left(\theta+60^{\circ}\right)+\cos \left(\theta+300^{\circ}\right)$.

Problem 25:(Year 2021, Problem 17)

Let $O$ be the circumcentre of the triangle $A B C$ and that $\angle A B C=30^{\circ}$. Let (D) be a point on the side (B C) such that the length of $A D$ is the same as the radius of the circle. Determine the value of $\angle A D O$ (in degree) if $\angle O A B=10^{\circ}$.

Problem 26: (Year 2021, Problem 19)

Find the value of

$\frac{1}{\sin ^2 0.5^{\circ}}-\tan ^2 0.5^{\circ}+\frac{1}{\sin ^2 1.5^{\circ}}-\tan ^2 1.5^{\circ}+\frac{1}{\sin ^2 2.5^{\circ}}-\tan ^2 2.5^{\circ}+\cdots+\frac{1}{\sin ^2 179.5^{\circ}}-\tan ^2 179.5^{\circ}$ .

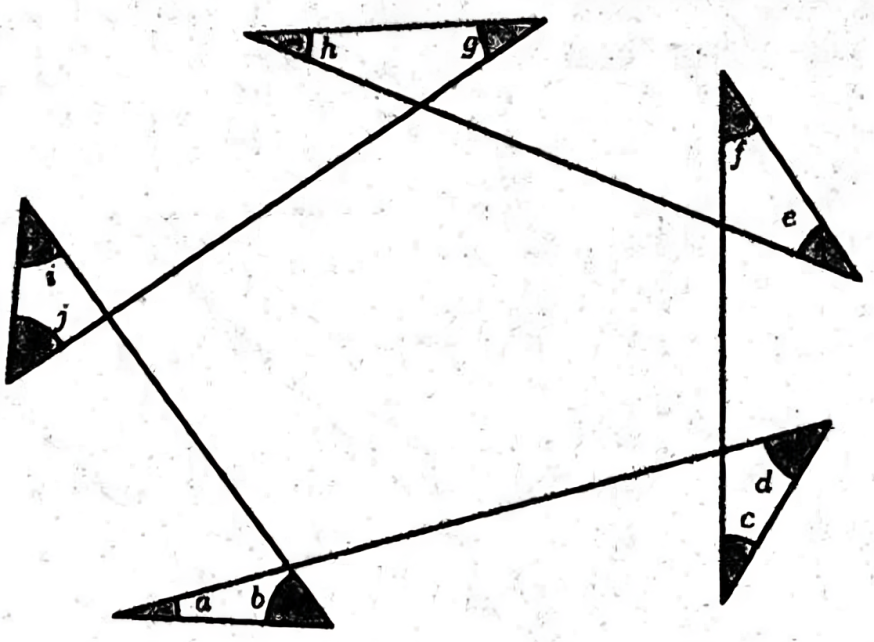
Problem 27:(Year 2021, Problem 21)

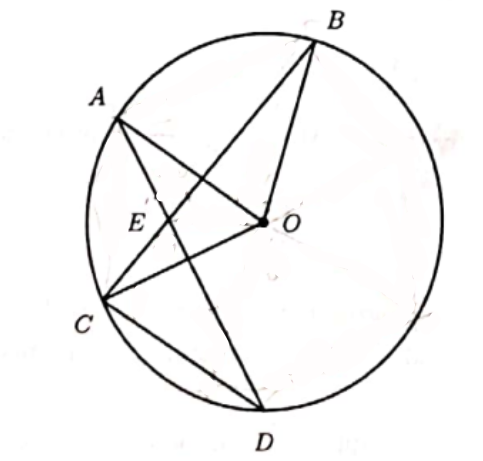
The figure below shows a circle centred at $O$ with radius $555 \mathrm{~cm}$. If $O A=O B$ and $\frac{R A}{A S}+\frac{R B}{B T}=\frac{13}{6}$, find $O A$ (in cm).

Problem 28:(Year 2020, Problem 7)

Parallelogram $A B C D$ has sides $A B=39 \mathrm{~cm}$ and $B C=25 \mathrm{~cm}$. Find the length of diagonal $A C$ in $\mathrm{cm}$ if diagonal $B D=34 \mathrm{~cm}$.

Problem 29: (Year 2020, Problem 08)

Suppose $\sin 45^{\circ}-x$=$-\frac{1}{3}$, where $45^{\circ}<x<90^{\circ}$. Find $6 \sin x-\sqrt{2})^2$.

Problem 30: (Year 2020, Problem 09)

If $8 \cos x-8 \sin x=3$, find the value of $55 \tan x+\frac{55}{\tan x}$.

Problem 31: (Year 2020, Problem 11)

The figure below shows a right-angled triangle $A B C$ such that $\angle B A C=90^{\circ}, \angle A B C=$ $30^{\circ}$ and $A B=48 \mathrm{~cm}$. Let $P$ be a point on side $A B$ such that $C P$ is the angle bisector of $\angle A C B$ and $Q$ be a point on side $B C$ such that line $A Q$ is perpendicular to line $C P$. Determine the length of $P Q$.

Problem 32:(Year 2020, Problem 12)

In the figure below, the point $O$ is the center of the circle, $A D$ and $B C$ intersect at $E$, and $\angle A E B=70^{\circ}, \angle A O B=62^{\circ}$. Find the angle $\angle O C D\left(\right.)$ in degree $\left.{ }^{\circ}\right)$.

Problem 33: (Year 2020, Problem 13)

Find the value of $\frac{4 \cos 43^{\circ}}{\sin 73^{\circ}}-\frac{12 \sin 43^{\circ}}{\sqrt{3} \sin 253^{\circ}}$.

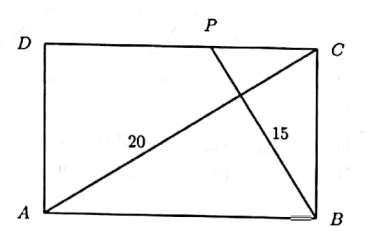
Problem 34: (Year 2020, Problem 20)

The figure below shows a rectangle (A B C D) such that the diagonal $A C=20 \mathrm{~cm}$. Let (P) be a point on side $C D$ such that $B P$ is perpendicular to diagonal $A C$. Find the area of rectangle $A B C D$ $in (\mathrm{cm}^2) $ if $B P=15 \mathrm{~cm}$.

Problem 35:(Year 2020, Problem 22)

Find the number of non-congruent right-angled triangles such that the length of all their sides are integers and that the hypotenuse has a length of $65 \mathrm{~cm}$.

Problem 36: (Year 2019, Problem 05)

Suppose that $\sin x=\frac{12}{13}$ and $\cos y=-\frac{4}{5}$, where $0^{\circ} \leq x \leq 90^{\circ}$ and $90^{\circ} \leq y \leq 180^{\circ}$. Find the value of $\cos (x+y)$.

(A) $-\frac{56}{65}$

(B) $\frac{56}{65}$

(D) $\frac{16}{65}$

(E) None of the above

Problem 37: (Year 2019, Problem 07)

Suppose $\tan x=5$. Find the value of $\frac{6+\sin 2 x}{1+\cos 2 x}$.

Problem 38:(Year 2019, Problem 09 )

The coordinates of the vertices of a triangle $\triangle A B C$ are $A(6,0), B(0,8)$ and $C(x, y)$ such that $x^2-16 x+y^2-12 y+91=0$. Find the largest possible value of the area of the triangle $\triangle A B C$.

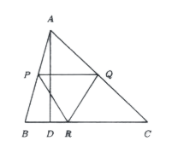
Problem 39:(Year 2019, Problem 10)

In the figure below, $A D$ is perpendicular to the $B C, P Q$ is parallel to $B C$, and the triangle $\triangle P Q R$ is an equilateral triangle whose area in $meter ^2$ is equal to the length of $A D$ (in meter). Find the smallest possible value of the length of (B C).

Problem 40: (Year 2019, Problem 11)

Find the value of $448\left(\frac{\sin 12^{\circ} \sin 39^{\circ} \sin 51^{\circ}}{\sin 24^{\circ}}\right)$.

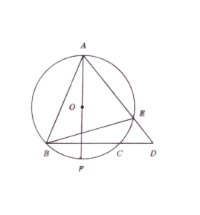
Problem 41:(Year 2019, Problem 12)

In the figure below, the chord $A F$ passes through the origin $O$ of the circle, and is perpendicular to the chord $B C$. It is given that $A B=17 \mathrm{~cm}, C D=5 \mathrm{~cm}$. Suppose $\frac{B E}{E D}=\frac{m}{n}$, where $m$ and $n$ are positive integers which are relatively prime. What is the value of $m+n$ ?

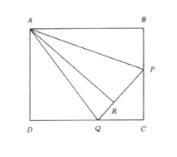
Problem 42:(Year 2019, Problem 19)

The figure below shows a rectangle $A B C D$ with $A B=16 \mathrm{~cm}) and (B C=15 \mathrm{~cm}$. Let $P$ be a point on the side $B C$ such that $B P=7 \mathrm{~cm}$, and let $Q$ be a point on the side $C D$ such that $C Q=6 \mathrm{~cm}$.
Find the length of $A R$ $in (\mathrm{cm})$, where $R$ is the foot of the perpendicular from $A$ to $P Q$.

Problem 43:(Year 2019, Problem 21)

Consider a square $A B C D$ on the $x y$-plane where the coordinates of its vertices are given by $A(13,0), B(23,13), C(10,23)$ and $D(0,10)$. A lattice point is a point with integer coordinates. Find the number of lattice points in the interior of the square.

Singapore Math Olympiad Past years Questions- Combinatorics (Senior)

Problem 01: (Year 2023, Problem 22)

Find the number of possible ways of arranging $m$ ones and $n$ zeros in a row such that there are in total $2 k+1$ strings of ones and zeros. For example, $1110001001110001$ consists of 4 strings of ones and 3 strings of zeros.

Problem 02: (Year 2021, Problem 23)

The following $3 \times 5$ rectangle consists of $151 \times 1$ squares. Determine the number of ways in which 9 out of the 15 squares are to be coloured in black such that every row and every column has an odd number of black squares.

Problem 03: (Year 2020, Problem 23)

There are 6 couples, each comprising a husband and a wife. Find the number of ways to divide the 6 couples into 3 teams such that each team has exactly 4 members, and that the husband and the wife from the same couple are in different teams.

Problem 04: (Year 2019, Problem 22)

Eleven distinct chemicals $C_1, C_2, \ldots, C_{11}$ are to be stored in three different warehouses. Each warehouse stores at least one chemical. A pair $C_i, C_j$ of chemicals, where $i \neq j$, is either compatible or incompatible. Any two incompatible chemicals cannot be stored in the same warehouse. However, a pair of compatible chemicals may or may not be stored in the same warehouse. Find the maximum possible number of pairs of incompatible chemicals that can be found among the stored chemicals.

Problem 05: (Year 2020, Problem 24)

Some students sat for a test. The first group of students scored an average of 91 marks and were given Grade A. The second group of students scored an average of 80 marks and were given Grade B. The last group of students scored an average of 70 marks and were given Grade $\mathrm{C}$. The numbers of students in all three groups are prime numbers and the total score of all the students is 1785 . Determine the total number of students.

Singapore Math Olympiad Past Years Question - Number Theory (Junior)

Problem 03: SMO Year-2023

The median and mean of five distinct numbers, (4,7,10,11, N), are equal. Find the sum of all possible values of (N).
(A) 18
(B) 21
(C) 26
(D) 29
(E) 35

Problem 07:SMO Year-2023

Let (n) be a positive integer such that (n+11) is a factor of (n^2+121). Find the largest possible value of (n).

Problem 08:SMO Year-2023

Find the largest integer less than or equal to $(3+\sqrt{5})^3$

Problem 09:SMO Year-2023

The product of the two-digit number $\overline{x 4}$ and the three-digit number $\overline{3 y z}$ is 7656 . Find the value of (x+y+z).

Problem 10:SMO Year-2023

If (x) and (y) are real numbers such that (x+y=12) and (x y=10), find the value of (x^4+y^4).

Problem 14:SMO Year-2023

Let (x) be a real number. What is the minimum value of the following expression?
$\frac{20 x^2+10 x+3}{2 x^2+x+1}$

Problem 01: SMO Year-2022

Which of the five numbers, $30^2, 10^3, 5^4, 4^5$ or $3^6$, is the largest?

(A) $30^2$
(B) $10^3$
(C) $5^4$
(D) $4^5$
(E) $3^6$

Problem 03: SMO Year-2022

The following diagram shows a system of balances hanging from the ceiling with three types of weights. The balances tip down to the heavier side. If we use $\square<\Delta$ to represent $\square$ is lighter than $\Delta$, which of the following is true?

Problem 07:SMO Year-2022

The digits (1,2,3,4,5) and 6 are arranged to form two positive integers with each digit appearing exactly once. How many ways can this be done if the sum of the two integers is 570 ?

Problem 12:SMO Year-2022

If (x) is a real number, how many solutions are there to the equation

$(3 x+2)^{x+5}=1 \text { ? }$

Problem 10:SMO Year-2023

The lengths of the sides of a triangle are $ \log_{10} 12$, $\log_{10} 75$ and $\log _{10}n$ where (n) is a positive integer. Find the number of possible values for (n).

Problem 17:SMO Year-2022

How many integers (n) are there in ${1,2, \ldots, 2022}$ such that at least one of the digits of $n$ is ' 2 '?

Problem 23:SMO Year-2022

How many integers (n) are there in ${1,2, \ldots, 2022}$ such that $\lfloor\sqrt[3]{n}\rfloor$ is a factor of $n$ ?

Problem 24:SMO Year-2022

If (x) and (y) can take any real values, what is the smallest possible value of the expression
$2 x^2+4 x y+5 y^2+4 x+10 y+13 ?$

Problem 08:SMO Year-2022

Consider the following product of two mixed fractions
$m\frac{6}{7} \times n \frac{1}{3}=23$,
where (m) and (n) are positive integers. What is the value of (m+n) ?

Problem 09:SMO Year-2022

What are the last four digits of the sum
$222+2022+20022+\cdots+2 \underbrace{0000000000}_{\text {ten } 0 s} 22$ ?

Give your answer as a 4-digit number.

Problem 01:SMO Year-2021

Let $a$ and $b$ be real numbers satisfying $a<0<b$. Which of the following is not true?

(A)$a^2 b<0$
(B) $a b^2<0$ (C) $\frac{a}{b}>0$
(D) $b-a>0$
(E) $|a-b|>0$

Problem 02:SMO Year-2021

The following diagram shows a system of balances hanging from the ceiling with three types of weights. The balances tip down to the heavier side. If we use $\square<\Delta$ to represent is lighter than $\triangle$, which of the following is true?

Problem 03:SMO Year-2021

Let $x=2^{20} \cdot 3^5, y=2^5 \cdot 5^{10}$ and $z=7^{10}$. Which of the following is true?
(A) $x>y>z$
(B) $x>z>y$
(C) $y>z>x$
(D) $y>x>z$
(E) $z>x>y$

Problem 05:SMO Year-2021

Which of the following is closest to the value of
$\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{3}}+\cdots+\frac{1}{\sqrt{2021}+\sqrt{2020}}$ ?
(A) 10
(B) 20
(C) 30
(D) 40
(E) 50

Problem 06:SMO Year-2021

Let $x$ be a positive integer. Suppose that the lowest common multiple of $x$ and $14$ is $42$ and the lowest common multiple of $x$ and $33$ is $66$ . What is the value of $x$ ?

Problem 07:SMO Year-2021

What are the last four digits of the sum
$1+22+333+4444+\cdots+\underbrace{999999999}_{\text {nine } 9 \mathrm{~s}} \text { ? A205 }$. Give your answer as a 4-digit number.

Problem 08:SMO Year-2021

ow many distinct triples of positive integers $(a, b, c)$ satisfy $1 \leqslant a \leqslant b \leqslant c$ and
$\frac{1}{a_3}+\frac{1}{b_3}+\frac{1}{c_3}=1 $ ?

Problem 14:SMO Year-2021

If $x$ is a 3-digit number, we define $M(x)$ and $m(x)$ respectively as the largest and smallest positive number that can be formed by rearranging the three digits of (x). For example, if $x=123$, then $M(123)=321$ and $m(123)=123$. If $y=898$, then $M(898)=988$ and $m(898)=889$.
Given that $z$ is a 3-digit number that satisfies $z=M(z)-m(z)$, what is the value of $z$ ?

Problem 19:SMO Year-2021

Let (x) be the positive real number that satisfies $\sqrt{x^2-4 x+5}+\sqrt{x^2+4 x+5}=3 x $.

What is the value of $\left\lfloor 10^4 x^2\right\rfloor$ ?

Problem 25:SMO Year-2021

Suppose a positive integer (x) satisfies the following equation
$\sqrt[5]{x+76638}-\sqrt[5]{x-76637}=5 $.

What is the value of $x$ ?

Problem 01:SMO Year-2020

Let $x=2^{300}, y=3^{200}$ and $z=6^{100}$. Which of the following is true?
(A) $x>y>z$
(B) $x>z>y$
(C) $y>z>x$
(D) $y>x>z$
(E) $z>x>y$

Problem 03:SMO Year-2020

(A) $\square<0<\triangle$
(B) $\square<\Delta<0$
(C) $\triangle<\square<0$
(D) $\triangle<0<\square$

Problem 04:SMO Year-2020

The integer 6 has exactly four positive factors, namely (1,2,3) and 6 . Likewise, the integer 8 has exactly four positive factors, (1,2,4) and 8 . How many integers from 9 to 50 (inclusive) have exactly four positive factors?
(A) 10
(B) 11
(C) 12
(D) 13
(E) 14

Problem 06:SMO Year-2020

Let (n) be a positive integer. Suppose the lowest common multiple of 4,5 and (n) is 2020 . What is the sum of the smallest possible value of (n) and the largest possible value of (n) ?

Problem 07:SMO Year-2020

When the five-digit integer $\overline{2 x 6 y x}$ is divided by the four-digit integer $\overline{5 y 27}$, the quotient is 4 and remainder is $\overline{x 106}$, which is a four-digit integer. What is the value of the digit (x) ?

Problem 09:SMO Year-2020

A quadruple ((a, b, c, d)) of positive integers is skewed if the median and mode of (a, b, c, d) are equal, but strictly greater than the mean of (a, b, c, d). How many skewed ((a, b, c, d)) of positive integers are there that satisfy $a \leq b \leq c \leq d$ and (a+b+c+d=40) ?

Problem 19:SMO Year-2020

Let $X=1234 \cdots 78798081$ be the integer that consists of all the integers from 1 to 81 written from left to right. What is the remainder of (X) when divided by 2020 ?

Problem 01:SMO Year-2019

Which of the five numbers $2^{30}, 3^{19}, 4^{14}, 6^{12}, 9^{10}$

has the largest value?

(A) $2^{30}$
(B) $3^{19}$
(C) $4^{14}$
(D) $6^{12}$
(E) $9^{10}$

Problem 04:SMO Year-2019

Let $x, y$ and $z$ be positive integers satisfying
$x^2+y^2+z^2=2(x y+1) \quad \text { and } \quad x+y+z=2022$ .

If $x_1$ and $x_2$ are two distinct solutions for $x$, what is the value of $x_1+x_2$ ?

(A) 2019
(B) 2020
(C) 2021
(D) 2022
(E) 2023

Problem 08:SMO Year-2019

Suppose that $m$ and $n$ are positive integers where $\frac{100 m}{n}$ is a perfect cube greater than 1 . What is the minimum value of $m+n$ ?

Problem 09:SMO Year-2019

What is the largest possible two-digit positive integer that is 18 more than the product of its two digits?

Problem 18:SMO Year-2019

A five-digit positive integer $x$ has the following properties:
(i) $x$ has distinct digits which are from ${1,2,3,4,5}$;
(ii) $x>23456$.

Problem 21:SMO Year-2019

A positive integer is said to be "twelvish" if the sum of digits in its decimal representation is equal to 12. For example, the first four twelvish integers are 39,48,57 and 66 . What is the total number of twelvish integers between 1 and 999 ?

Singapore Math Olympiad Past Years Question - Algebra (Junior)

Problem 06:SMO Year 2023

The product of the ages of three adults is 26390 . Find the sum of their ages. (A person is an adult if he or she is at least 21 years old.)

Problem 09:SMO Year 2023

The product of the two-digit number $\overline{x 4}$ and the three-digit number $\overline{3 y z}$ is 7656 . Find the value of (x+y+z).

Problem 10:SMO Year 2023

If (x) and (y) are real numbers such that (x+y=12) and (x y=10), find the value of (x^4+y^4).

Problem 12:SMO Year 2023

Find the value of the integer (n) such that the following equation holds:
$[
\frac{\sqrt{5}+n \sqrt{3}-2 \sqrt{2}}{(\sqrt{5}+\sqrt{3})(\sqrt{3}-\sqrt{2})}=\sqrt{5}+\sqrt{2} .
]$

Problem 14:SMO Year 2023

Let (x) be a real number. What is the minimum value of the following expression?
$[
\frac{20 x^2+10 x+3}{2 x^2+x+1}
]$

Problem 19:SMO Year 2023

If $\sqrt{19-8 \sqrt{3}}$ is a root of the equation (x^2-a x+b=0) where (a) and (b) are rational numbers, find the value of (a+b).

Problem 24:SMO Year 2023

Four positive integers (x, y, z) and (w) satisfy the following equations:
$[
\begin{aligned}
& x y+x+y=104 \
& y z+y+z=146 \
& z w+z+w=524
\end{aligned}
]$

Problem 08:SMO Year 2021

Consider the following product of two mixed fractions
$m\frac{6}{7} \times n \frac{1}{3}=23$,
where (m) and (n) are positive integers. What is the value of (m+n) ?

Problem 10:SMO Year 2021

If (a) and (b) are distinct solutions to the equation
$x^2+10 x+20=0$,
what is the value of $a^4+b^4$ ?

Problem 22:SMO Year 2021

If we have
$\frac{\sqrt{15}+\sqrt{35}+\sqrt{21}+5}{\sqrt{3}+2 \sqrt{5}+\sqrt{7}}=\frac{a \sqrt{7}+b \sqrt{5}+c \sqrt{3}}{2}$
for some integers (a, b, c). What is the value of (a+b+c) ?

Problem 15:SMO Year 2021

How many integers (k) are there such that the quadratic equation $k x^2+20 x+20-k=0$ has only integer solutions?

Problem 19:SMO Year 2021

Let (x) be the positive real number that satisfies $\sqrt{x^2-4 x+5}+\sqrt{x^2+4 x+5}=3 x $.

What is the value of $\left\lfloor 10^4 x^2\right\rfloor$ ?

Problem 20:SMO Year 2021

What is the number of positive integers (c) such that the equation $x^2-2021 x+100 c=0$ has real roots?

Problem 20:SMO Year 2020

Let $A=\frac{1}{7} \times 3.14 \mathrm{i} \dot{5}), where (3.14 \mathrm{i} \dot{5}$ is the rational number with recurring digits 15 . In other words,
$[
3.14 \dot{1} \dot{5}=3.14+0.0015+0.000015+0.00000015+\cdots .
]$ Suppose that $A=\frac{m}{n}$, where (m) and (n) are positive integers with no common factors larger than 1 . What is the value of (m+n) ?

Problem 22:SMO Year 2020

If we have
$[
(1-3 x)+(1-3 x)^2+\cdots+(1-3 x)^{100}=a_0+a_1 x+a_2 x^2+\cdots+a_{100} x^{100},
]$
for some integers (a_0, a_1, \ldots, a_{100}), what is the value of
$[
\left|\frac{a_1}{3}+\frac{a_2}{3^2}+\cdots+\frac{a_{100}}{3^{100}}\right| ?
]$

Problem 25:SMO Year 2020

What is the value of
$[
\begin{aligned}
\left(\frac{1}{2}+\frac{1}{3}\right. & \left.+\frac{1}{4}+\frac{1}{5}+\cdots+\frac{1}{37}\right)+\left(\frac{2}{3}+\frac{2}{4}+\frac{2}{5}+\cdots+\frac{2}{37}\right) \
& +\left(\frac{3}{4}+\frac{3}{5}+\frac{3}{6}+\cdots+\frac{3}{37}\right)+\cdots+\left(\frac{35}{36}+\frac{35}{37}\right)+\frac{36}{37} ?
\end{aligned}
]$

Problem 04:SMO Year 2019

Let $x, y$ and $z$ be positive integers satisfying
$x^2+y^2+z^2=2(x y+1) \quad \text { and } \quad x+y+z=2022$ .

If $x_1$ and $x_2$ are two distinct solutions for $x$, what is the value of $x_1+x_2$ ?

Problem 8:SMO Year 2019

Suppose that $m$ and $n$ are positive integers where $\frac{100 m}{n}$ is a perfect cube greater than 1 . What is the minimum value of $m+n$ ?

Problem 16:SMO Year 2019

If the equation $\frac{x-1}{x-5}=\frac{m}{10-2 x}$ has no solutions in $x$, what is the value of $|m| ?$

Problem 20:SMO Year 2019

If (x) is a nonnegative real number, find the minimum value of
\[
\sqrt{x^2+4}+\sqrt{x^2-24 x+153} .
\]

Singapore Math Olympiad Past ears Questions- Combinatorics (Junior)

Problem 04 - SMO Year 2022

A shop sells two types of buns, with either cream or jam filling, which are indistinguishable until someone bites into the buns. Four mathematicians visited the shop and ordered (not necessarily in that sequence): three cream buns, two cream buns and one jam bun, one cream and two jam buns, and three jam buns. Each knew precisely what the others had ordered. Unfortunately, the shop owner mixed up the orders and gave each mathematician the wrong order!
The mathematicians started eating, all still unaware of the mixup, until the shop owner ran over to inform them of the mistake. Mathematician A said: "I ate two buns and both had cream filling. So, if my order was wrong, I now know what type my third bun is." Mathematician B then said: "I only ate one bun and it had cream filling. Based on what A said and since I remember A's order, I now know what type my other two buns are." Finally, Mathematician C said: "I have not started eating but I must have received three jam buns." Which of the following statements about Mathematician D is correct?

(A) D ordered two cream and one jam but received three jam buns.
(B) D ordered one cream and two jam but received two cream and one jam buns.
(C) D ordered three cream but received one cream and two jam buns.
(D) D ordered three jam but received three cream buns.
(E) None of the above

Problem 07- SMO Year 2022

The digits (1,2,3,4,5) and 6 are arranged to form two positive integers with each digit appearing exactly once. How many ways can this be done if the sum of the two integers is 570 ?

Problem 13 - SMO Year 2022

In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If $\mathrm{W}$ represents 5 , what number does TROOP represent?

Problem 16 - SMO Year 2022

Eggs in a certain supermarket are sold only in trays containing exactly 10,12 or 30 eggs per tray. It is thus impossible to buy exactly 14 eggs or any odd number of eggs. However, it is possible to buy exactly 78 eggs using four trays of 12 and one tray of 30 . What is the largest even number of eggs that is impossible to be bought from this supermarket?

Problem 11 - SMO Year 2021:

In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If $S$ represents $6 $and $E$ represents $8$,-what number does SIX represent?

Problem 21 - SMO Year 2021

In chess, two queens are said to be attacking each other if they are positioned in the same row, column or diagonal on a chessboard. How many ways are there to place two identical queens in a (4 \times 4) chessboard such that they do not attack each other?
$\frac{1}{2} \times \frac{1}{4} \times 401 \times 403 x \times 801=$

Problem 23 - SMO Year 2021:

A $3 \times 3$ grid is filled with the integers 1 to 9 . An arrangement is nicely ordered if the integers in each horizontal row is increasing from left to right and the integers in each vertical column is increasing from top to bottom. Two examples of nicely ordered arrangements are given in the diagram below. What is the total number of distinct nicely ordered arrangements?

Problem 24 - SMO Year 2021:

A class has exactly 50 students and it is known that 40 students scored (A) in English, 45 scored (A) in Mathematics and 42 scored (A) in Science. What is the minimum number students who scored (A) in all three subjects?

Problem 02 - SMO Year 2020:

An expensive painting was stolen and the police rounded up five suspects Alfred, Boris, Chucky, Dan and Eddie. These were the statements that were recorded.
Alfred: "Either Boris or Dan stole the painting."
Boris: "I think Dan or Eddie is the guilty party."
Chucky: "It must be Dan."
Dan: "Boris or Eddie did it!"
Eddie: "I am absolutely sure the thief is Alfred."
The police knew that only one of the five suspects stole the painting and that all five were lying. Who stole the painting?
(A) Alfred
(B) Boris
(C) Chucky
(D) Dan
(E) Eddie

Problem 12 - SMO Year 2020:

In the figure below, each distinct letter represents a unique distinct digit such that the arithmetic holds. If the letter K represents 6 , what number does SHAKE represent?

Problem 21- SMO Year 2020:

Ali and Barry went running on a standard 400 metre track. They started simultaneously at the same location on the track but ran in opposite directions. Coincidentally, after 24 minutes, they ended at the same location where they started. Ali completed 12 rounds of the track in those 24 minutes while Barry completed 10 rounds. How many times did Ali and Barry pass each other during the run? (Exclude from your answer the times that they met at the start of the of run and when they completed the run after 24 minutes.)

Problem 2 - SMO Year 2019

In a strange island. there are only two types of inhabitants: truth-tellers who only tell the truth and liars who only tell lies. One day, you meet two such inhabitants $A$ and $B$. $A$ said "Exactly one of us is a truth teller." $B$ kept silent. Which of the following must be true?

(A) Both $A$ and $B$ are truth-tellers
(B) Both $A$ and $B$ are liars
(C) $A$ is a truth-teller and $B$ is a liar
(D) $A$ is a liar and $B$ is a truth-teller
(E) Not enough information to decide

Problem 19 - SMO Year 2019

In the figure below, each distinct letter represents a unique digit such that the arithmetic holds. What digit does the letter $\mathrm{L}$ represent?

Problem 22 - SMo Year 2019

Two secondary one and $m$ secondary two students took part in a round-robin chess tournament. In other words, each student played with every other student exactly once. For each match, the winner receives 3 points and the loser 0 points. If a match ends in a draw, both contestants receive 1 point each. If the total number of points received by all students was 130 , and the number of matches that ended in a draw was less than half of the total number of matches played, what is the value of $m$ ?

Singapore Math Olympiad Past Years Questions- Geometry (Junior)

Problem 02 - SMO Year 2023:

How many non-congruent triangles with integer side lengths have perimeter 7 ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5

Problem 04 - SMO Year 2023:

The following diagram shows two semicircles whose diameters lie on the same line. (A B) is a chord of the larger semicircle that is tangent to the smaller semicircle at the point $\mathrm{C}$ and is parallel to the diameter $\mathrm{DE}$ of the larger semicircle. If $|\mathrm{AB}|=16 \mathrm{~cm}$, what is the area of the shaded region in $\mathrm{cm}^2$ ?

(A) $8 \pi$
(B) $16 \pi$
(C) $32 \pi$
(D) $48 \pi$

Problem 15 - SMO Year 2023:

In the following diagram, $\mathrm{ABCD}$ is a square of side $16 \mathrm{~cm}$. $\mathrm{E}$ lies on $\mathrm{CD}$ such that $|\mathrm{DE}|=) (4 \mathrm{~cm} . \mathrm{M}) and (\mathrm{N}$ lie on $\mathrm{AD}$ and $\mathrm{BC}$ respectively such that $\mathrm{MN}$ is perpendicular to $\mathrm{BE} . \mathrm{X}$ is the intersection of $\mathrm{MN}$ and $\mathrm{BE}). If (|\mathrm{MX}|=11 \mathrm{~cm}$ and $|\mathrm{BN}|=x \mathrm{~cm}$, what is the value of (x) ?

Problem 18 - SMO Year 2023:

The sum of all the interior angles except one of a convex polygon is $2023^{\circ}$. What is the number of sides of this polygon? (A polygon is convex if every interior angle is between $0^{\circ}$ and $180^{\circ}).$

Problem 21 - SMO Year 2023:

In the following diagram, (A B) is parallel to $\mathrm{DC},|\mathrm{AB}|=6 \mathrm{~cm},|\mathrm{AD}|=17 \mathrm{~cm},|\mathrm{DC}|=10 \mathrm{~cm}$ and angle $\mathrm{DAB}=90^{\circ}$. $\mathrm{E}$ lies on $\mathrm{AD}$ such that $\mathrm{BE}$ is perpendicular to $\mathrm{EC}$. If the area of triangle $\mathrm{BEC}=k \mathrm{~cm}^2$, what is the largest possible value of (k) ?

Problem 11- SMO Year 2022

The following diagram shows a star that is cut out from a square with sides of length 30 . What is the area enclosed by the star?

Problem 14 - SMO Year 2022

In the following diagram, a white square and four grey squares of equal size are drawn in a circle such that both dashed lines form diameters of the circle. If the diameter has length 60 , find the smallest possible value for the total area of the five squares.

Problem 19 - SMO Year 2022

In the following diagram, (A C D) is a triangle such that $|A B|=|B C|, \angle A B D=45^{\circ}) and (\angle B D C=15^{\circ}$. If $\angle A D B=x^{\circ}$, what is the value of $x$ ?

Problem 20 - SMO Year 2022

What is the area of a triangle with side lengths
$\sqrt{6^2+7^2}, \sqrt{12^2+7^2} \text { and } \sqrt{6^2+14^2} \text { ? }$

Problem 25 - SMO Year 2022

The following diagram shows a rectangle that is partitioned into 17 squares. If the two smallest squares, shaded in grey, have sides of length 2 , what is the area of the rectangle?

Problem 04 - SMO Year 2021:

In the diagram, six circles are tangent to each other. If the radius of the largest circle is 1 and the radii of the four medium sized circles are equal, what is the radius of the smallest circle?

(A) $\sqrt{2}-1$

(B) $3-2 \sqrt{2}$

(D) $6-4 \sqrt{2}$

(E) None of the above

Problem 16 - SMO Year 2021:

In the following diagram, $A B C D$ is a quadrilateral inscribed in a circle with center $O$. If $|A B|=|B C|=6,|A D|=14$ and $C D$ is a diameter, what is the length of $|C D|$ ?

Problem 17 - SMO Year 2021:

The diagram below shows a piece of cardboard in the shape of an equilateral triangle with side length $36 \mathrm{~cm}$. Six perpendicular cuts of length $2 \sqrt{3} \mathrm{~cm}$ are made to remove the corners in order to fold the cardboard into a tray whose base is an equilateral triangle and height is $2 \sqrt{3} \mathrm{~cm}$. What is the volume of the tray in $\mathrm{cm}^3$ ?

Problem 11 - SMO Year 2020:

Let (A B C) be a triangle where (D) is the midpoint of (B C) and (E) lies on (A C) such that (A E: E C=3: 1). Let (F) be the intersection of (A D) and (B E). If the area of (A B C) is 280 , what is the area of triangle (B F D) ?

Problem 17 - SMO Year 2020:

In the following diagram, (A B C D) is a rectangle where (E) and (F) are points on (B C) and (C D) respectively. The area of triangle (A E F), denoted ([A E F]), is 2037 . If
$[
[A E C F]=2[A B E]=3[A D F],
]$
what is the area of the rectangle (A B C D) ?

Problem 18 - SMO Year 2020:

In the following diagram, (A B C D) is a square of side length (64 . E) is the midpoint of (A B), (F) is the midpoint of (E C) and (G) is the midpoint of (F D). What is the area enclosed by the quadrilateral (A E F G) ?

Problem 5 - SMO Year 2019:

In a quadrilateral $A B C D$, the diagonals $A C$ and $B D$ intersect at the point $O$. Suppose that $\angle B A D+\angle A C B=180^{\circ},|B C|=3,|A D|=4,|A C|=5$ and $|A B|=6$. What is the value of $\frac{|O D|}{|O B|}$ ?

(A) $\frac{2}{3}$
(B) $\frac{8}{9}$
(C) $\frac{9}{10}$

Problem 6 - SMO Year 2019

In the following diagram, all lines are straight. What is the value $\left(\right.$ in $\left.^{\circ}\right)$ of
\[
\angle a+\angle b+\angle c+\angle d+\angle e+\angle f+\angle g+\angle h+\angle i+\angle j ?
\]

Problem 11 - SMO Year 2019

In the following diagram, $A B C D$ is a rectangle with $|A B|=4$ and $|B C|=6$. Points $E$ and $F$ lie on the sides $B C$ and $A D$ respectively such that $|B E|=|F D|=2$. Points $G$ and $H$ lie on the sides $A B$ and $C D$ respectively such that $|A G|=|C H|=1$. Suppose $P$ lies on $E F$, such that the quadrilateral $B G P E$ has area 5 . What is the area of the quadrilateral $F D H P ?$

Problem 13 - SMO Year 2019

In the following diagram, $A B C D, A C F E$ and $E C H G$ are all rectangles. If $|A B|=6$ and $|B C|=8$, what is area of the rectangle $E C H G$ ?

Problem 23 - SMO year 2019

$A B C D$ is a square sheet of paper with sides of length 6 . The paper is folded along a crease line $E F$ so that points $A$ and $B$ now lie on $A^{\prime}$ and $B^{\prime}$ respectively as indicated in the diagram. If $H$ is the intersection of $A^{\prime} B^{\prime}$ and $B C$, what is the perimeter of the triangle $A^{\prime} C H$?

Problem 24 - SMO Year 2019

In the following diagram, $\angle B E D=30^{\circ}$ and $\angle D B E=15^{\circ}$. If $|C D|=|D E|$, what is the value of $x$ ?

Problem 25 - SMO Year 2019

In the following diagram, $P_1, P_2, \cdots, P_8$ are points on $\triangle A B C$ such that
$
\left|A P_1\right|=\left|A P_8\right|=\left|P_i P_{i+1}\right|, \text { for all } i=1,2, \cdots, 7 .
$

What is the value $in ({ }^{\circ}) $ of $\angle B A C$ ?