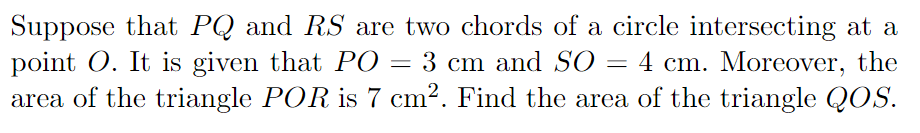Inspired by the book of Precalculus written in a dialogue format by L.V.Tarasov, I also wanted to express myself in a similar fashion when I found that the process of teaching and sharing knowledge in an easy way is nothing but the output of a lucid conversation between a student and a teacher inside the person only.
Instead of presenting in paragraphs, I will express that discussion in the raw format of conversation to you.
Student: Do you think problem - solving is so important in learning math?
Teacher: Yes, surely without problem-solving, you will not at all enjoy the process of learning of mathematics. If you learn math without problem-solving is like charging the phone without the battery.
S: But why is it so important?
T: Math is nothing but layers of answers to a large number of Whys, Hows, Can We, etc. All the thoughts, questions and answers are refined into something called theorems and lemmas to make them look concise. Theory develops in this way only. Often someone gives a new way of looking into things or connecting two different fields of study, that becomes the definitions, but that was actually done to solve a new problem or question that occurred in their minds or make the things precise. Problems and Theory are the two sides of the same coin.
S: Interesting! So, a student how can we build our own new theory?
T: That's a good question. As I told you, it is about not developing a new theory, it is about solving a new problem always. So find your own problems or existing ones and start spending time with them.
S: What if I couldn't solve a problem?
T: That is the best part when you solve problems. You try to understand what doesn't work. You have to understand why it doesn't work. Then only you can engineer an alternate pathway, and that is eventually called a new theory if it is too influential. But whatever you have thought you can call it your own theory. Even if you cannot develop a full alternated pathway, something new you have thought will help you solve another problem you were pondering upon for sometime. This actually happenned with me.
S: Wow! This problem solving path seems to be quite adventurous. I never thought it this way.
T: Yes, it is. Infact human beings think and behave in this way only, when their rational and logical part of the brain work. Only they have to conscious of the steps they are taking and they have to take the opportunity to learn at every failure.
S: So, are there any problem solving tips for me?
T: I really don't believe in tricks while learning, tricks are important for quick problem solving that is only required in the exam. But those are temporary. Once you develop your own strategies, first of all we will get to know something new from you and also you will never forget those strategies. But yes, from my experience I can help you in approaching problems.
S: Surely, what are they?
T: First of all, you need to understand the working principle of problem-solving. It works like whenever you think or see some problem, you are either blank or you have some ideas to approach based on your previous experiences and knowledge.
S: Yes, then?
T: Well, if you have some ideas, you approach along that path till you can't proceed further. You have to find everytime where is the problem occurring and how to bypass it. This is why different people have different solutions to a problem because they create different bypasses.
S: What if I am blank?
T: You have to learn how to bring in ideas into you.
S: But how?
T: First of all, without knowledge or past experience ideas will rarely come, because that is how humans think using past data. Do you that our visual memory is the maximum memory among all the senses?
S: I felt that was true, but I knew that. But how is it related to math and problem-solving?
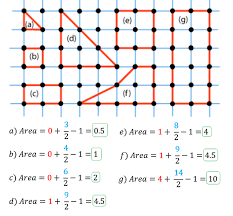
T: well, try to draw a picture in your mind or your copy. Try to draw a mindmap, some flowcharts to get some visual aspect of the theory or the problems. Now your visual memory comes into play automatically. That's why, the important step when you learn something new or try to solve something, ALWAYS TRY TO DRAW DIAGRAMS AND PICTURES WHENEVER IT IS POSSIBLE.
S: That's seems quite satisfying. I will start doing it from today only. What else?
T: Actually this is the first and important step. Also, intuition is also gained by the method of HIT AND TRIAL. When you have a problem, you play with the numbers in the problem or the expressions and often it happened to me that something interesting came out. So, also whenever you are blank, you can follow this HIT AND TRIAL methodology to start your idea engines and this helps you in recognizing patterns.
S: Hit and Trial seems exciting and adventurous too. What did you mean by pattern recognition?
T: Pattern recognition is the most important part of math. You have to observe a pattern and justify it with logic in a new problem. The first step to problem-solving is to find the pattern. Then comes the next part of logically justifying the pattern. To help you see the pattern and proceeding through you are guided by DRAWING PICTURES and HIT AND TRIAL methodologies.
S: What about logically justifying a problem?
T: This is the most difficult part and rewarding part of mathematics. Often people are not being properly trained in this domain that's why they find it uninteresting. The method of proofs depends on the pattern you see and observe and that varies from person to person. But proving that the pattern actually holds requires some serious training. Isn't it so beautiful, when you show that what you observe actually works? It is like painting your patterns by the brush of logic.
S: How do I develop that?
T: That is solely practice and you must enjoy that process. That process requires some knowledge and how people approached on similar ideas and patterns. Once you develop that habit, you will find it super rewarding. It is also a continuously learning path.
S: How do we learn like that that interesting way?
T: Yes, that is a really nice question and those who can impart this knowledge into you very fluidly and interestingly are good teachers. If you want to be a good teacher, you have to start practicing that too. You have to understand and question why every step works and are there any other ways to do it? Then only you will learn out of a problem, or a solution you have learned. Even if you are learning, you have to question WHY THIS WAY AND NOT THAT WAY. Develop the habit of questioning at every step of your learning process, then only you will enjoy.
S: Nice! I learnt a lot of new things today. Let me put that into action. See you later. Have a nice day.
T: Yes, you must put them into action. Yes see ya later. Have a nice day. Bye.
S: Bye.