NOAI 2024 China

Basket Ball Shooting

I. Question Overview

A CSV file of basketball stars' shooting data is given, which is stored in the training set data_train.csv. The meaningful variables are named as follows:

Now, it is hoped that you can build a model based on the historical data of the basketball star to predict the shooting result of the star. There are 20,000 data points in the training set, and the test set has approximately 5,000 data points. The format is similar to that of the training set, and the contestants cannot access it during the competition.

II. Data Set

Address of the training set: Training Set.

III. Task

Please use PyTorch to implement a multi-layer perceptron (neural network) model to predict whether a contestant can make a shot at different positions. The specific requirements are as follows:

  1. The input consists of 2 features (loc_x, loc_y), and the output is 1 label (shot_made_flag). 1 indicates that the shot is made, and 0 indicates that the shot is missed.
  2. Only linear layers and activation functions after linear layers can be used, and at most 3 linear layers can be used. Please build the neural network directly and do not use nn.Sequential() nesting. The scoring system cannot detect the network structure inside nn.Sequential(), and a score of 0 will be directly given.
  3. The activation function can only be selected from nn.Linear, nn.ReLU, nn.Sigmoid, nn.Tanh, nn.ELU, nn.LeakyReLU, nn.PreLU. Each linear layer can have at most 8 neurons.
  4. The loss function, optimizer (solver), and learning rate can be freely selected.

IV. Submission

Please submit a compressed file named submission.zip. After decompression, it should contain the model file submission_model.py and the model parameter file submission_dic.pth. The specific requirements are as follows:

  1. Save the class definition of the model and the required precursor libraries in submission_model.py.
  2. Save the trained model parameters in submission_dic.pth. The model parameters will be loaded during scoring.
  3. You can refer to the method in baseline.ipynb to generate the submission.zip file on the platform for submission. You can also download the data set to the local machine, train the model, and then package it into a submission.zip file for submission.

Address of baseline.ipynb: Question 1 of APOAI2025 Mock Competition_baseline.

V. Scoring

  1. When the number of linear layers and the number of neurons in the neural network meet the requirements, the score is the accuracy rate of the test set.
  2. When the number of linear layers and the number of neurons in the neural network do not meet the requirements, the score is 0.

    Remarks: The leaderboard A uses 50% of the data in the test set, which can be displayed in real time during the competition to help contestants debug the model. The leaderboard B uses the remaining 50% of the data in the test set and is calculated after the competition ends. The score of the leaderboard B is the final score.

NOAI 2024 China - News Text Classification Task

I. Question Overview

A dataset for news text classification is provided, which is stored in a .csv file and contains two variables:

The training set is stored in train_news.csv, with a total of 1,000 samples. The testing set is stored in test_news.csv, with a total of 200 samples. During the competition, the test set samples without labels will be provided.

II. Data Set

  1. Address of the training set: train_news.csv, Training Set;
  2. Test set (without labels): test_news_nolabel.csv, which contestants cannot access or download;
  3. Test set (with labels): test_news_label.csv, which contestants cannot access or download.

III. Task

Please use PyTorch to design and train a natural language processing model to achieve the news text classification task, that is, input the sentences of the news and output the news categories.

The specific requirements are as follows:

  1. The total training time and testing time using the CPU should not exceed 10 minutes. The connection time and queuing time are not counted into the total time.
  2. Tip: It is recommended to use Word Embedding + LSTM.

IV. Submission

Please submit the submission.ipynb file, which contains the entire process of training the model. In submission.ipynb, store the prediction results of the test set in submission.csv. The naming and storage method of the label should be consistent with that of train_news.csv.

You can refer to the submission format in baseline.ipynb. The address of baseline.ipynb: Question 3 of APOAI Mock Competition_baseline.

V. Scoring

  1. When the training and testing are completed within the specified time, the scoring criterion is the average value of the F1-Scores of all categories. Please look up the meaning of F1-Score on the Internet by yourself.
  2. If the F1-Scores of all categories are not calculated, a score of 0 will be given.
  3. If the total time for training and testing exceeds the time limit, a score of 0 will be given.

NOAI 2024 China - Pendulum Motion with Missing Data

I. Question Overview

A dataset for pendulum motion is provided, which is stored in a .csv file and contains two variables:

Based on the above dataset, please use PyTorch to regress the relevant parameters of the pendulum motion with resistance, fill in the missing data and make predictions.

II. Data Set

There are three datasets.

  1. Training set: pendulum_train.csv, Address of the training set: Training Set;
  2. Test set A: pendulum_testA.csv. Contestants cannot directly download Test set A during the competition;
  3. Test set B: pendulum_testB.csv. Contestants cannot directly download Test set B during the competition.

The data in the training set is all visible, which can help contestants generate methods for solving parameters. The data of Test set A is invisible to contestants, but it will be displayed in the Leaderboard A, which can help contestants verify whether the method for solving parameters is correct. The data of Test set B is invisible to contestants and will finally be used when calculating scores in the Leaderboard B.

Note: The differential equation parameters of the training set, Test set A and Test set B are all different. What contestants need to submit is a solution method that can be applied to different data. When importing different data sets, that is, when importing the training set, Test set A and Test set B, the correct parameters can be solved.

III. Task

In machine learning, we sometimes encounter scenarios where we need to extract the patterns in data with a small amount of data. In such scenarios, how to make full use of prior knowledge (formulas) to process data, design models and successfully solve unknown parameters is the key to solving the problem. Now consider a pendulum scenario.

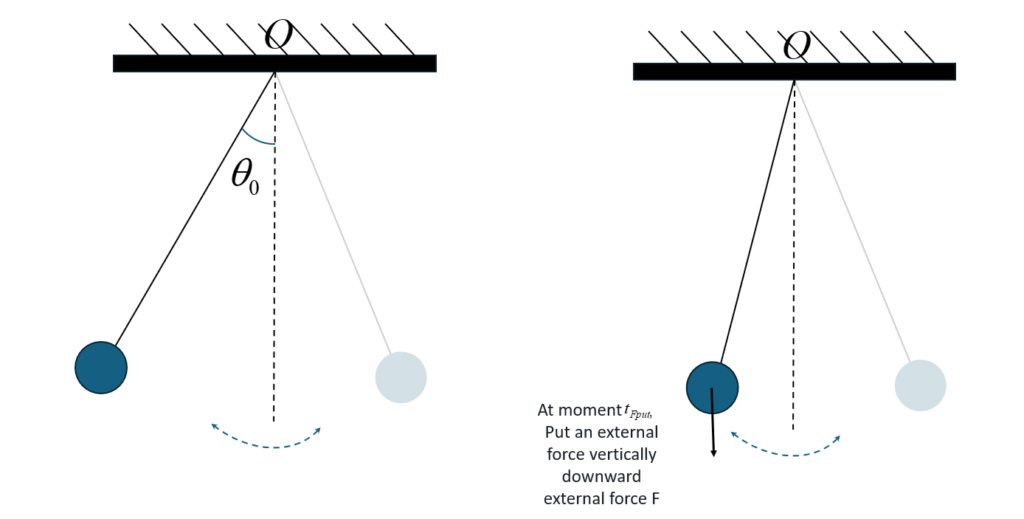
As shown in the above figure, there is a small ball with a mass of 1$(m=1)$that can be regarded as a particle, which is suspended by a light rope with a length of $l$ at a fixed point $O$. Let $\theta(t)$ be the angle between the rope and the vertical line passing through $O$ at time $t$, which is called the pendulum angle.

Stretch the rope straight and release the small ball with an initial pendulum angle $\theta_0<\pi / 2$ (in radian measure). If you don't understand radian measure, you can ask a large language model). At $t=0$, release the small ball without an initial velocity, and then the small ball can move in the plane corresponding to the light rope and the vertical line. Here, taking the initial pendulum angle $\theta_0$ as positive, when the small ball is on the left side of the vertical line, the sign of the pendulum angle$\theta(t)$ is recorded as positive, and when it is on the right side of the vertical line, the sign of the pendulum angle $\theta(t)$ ) is recorded as negative.

Let the acceleration due to gravity be $g=9.8$ (during the whole problem-solving process, there is no need to consider unit conversion, and you can directly operate on the numerical values).

Consider the air resistance whose magnitude is proportional to the velocity and whose direction is opposite to the velocity, and the magnitude of the air resistance $\mu$ remains constant during the motion.

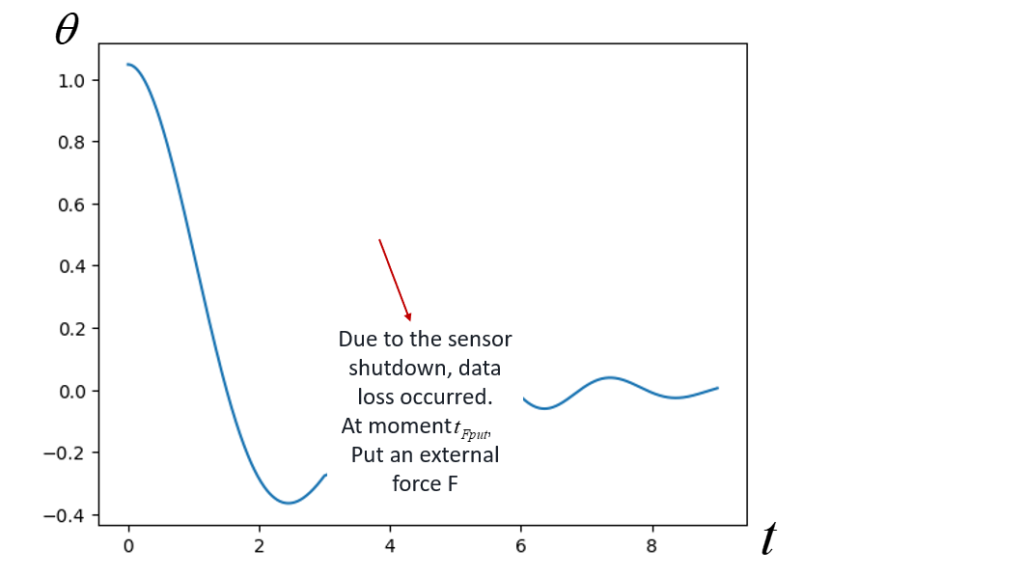
There is a sensor that can accurately record the pendulum angle of the small ball. However, during the experiment, the sensor had a problem. It suddenly interrupted for several seconds ( $\geq 1 s$ ) during the recording and was restarted only after that, and it stopped working before the small ball stopped moving. It is known that starting from a certain moment $t_{F_{\text {put }}}$ during the interrupted period, the small ball was subjected to a constant external force $F$ in the vertical downward direction, and this continued until the end of the motion.

There is a sensor that can accurately record the pendulum angle of the small ball. However, during the experiment, the sensor had a problem. It suddenly interrupted for several seconds ( $\geq 1 s$ ) during the recording and was restarted only after that, and it stopped working before the small ball stopped moving. It is known that starting from a certain moment $t_{F_{\text {put }}}$ during the interrupted period, the small ball was subjected to a constant external force $F$ in the vertical downward direction, and this continued until the end of the motion.

Please try to infer and predict the situation of the small ball based on the recorded data. The data is in the .csv file, which includes two columns. The first column records the time stamp $t$ of the small ball's motion, represented by the variable t , and the second column records the pendulum angle information $\theta$ of the small ball, represented by the variable theta. We plot the pendulum angle data $\theta(t)$ in the training set as follows:

To solve this problem, you need to have prior knowledge of differential equations. During the whole motion process, the angular velocity $\omega(t)$ refers to the instantaneous change rate of $\theta(t)$ (with positive and negative values), and the angular acceleration $a(t)$ refers to the instantaneous change rate of the angular velocity $\omega(t)$ (with positive and negative values), that is, $\omega(t)=\frac{d \theta(t)}{d t}, a(t)=\frac{d \omega(t)}{d t}$ (if you don't understand derivatives, you can ask a large language model). Then, in the above pendulum problem, $a(t)$ should satisfy the following differential equation with $\omega(t)$ and $\theta(t)$ :

$$
a(t)=-\alpha \cdot \omega(t)-\beta \sin (\theta(t)),
$$

where $\alpha$ and $\beta$ are parameters. According to Newton's second law,

When $t \geq t_{F_{\text {put }}}$ an external force $F$ is applied. At this time, $\beta=\beta_2=\frac{g}{l}+\frac{F}{m l}$.

Using the differential equation, if $\alpha_{,} \beta_1$, and $\beta_2$ are known, when the angular velocity $\omega(t)$ and the pendulum angle $\theta(t)$ at time $t$ are known, $a(t)$ can be calculated according to the differential equation.

However, the problem in this question is that $\alpha, \beta_1$, and $\beta_2$ are unknown, and only the pendulum angle data $\theta(t)$ recorded at each moment is available. You need to "regress" $\alpha, \beta_1$, and $\beta_2$ according to the provided data. This is the core task in this question.

After obtaining $\alpha, \beta_1$, and $\beta_2$, it is equivalent to obtaining the entire differential equation, and then you can use the differential equation to complete and predict the pendulum angle data of the small ball.

Specifically, you need to solve the following parameters according to the time $t$ and $\theta(t)$ data recorded in the .csv file:

  1. The length of the rope: $l$;
  2. The air resistance: $\boldsymbol{\mu}$;
  3. The magnitude of the external force applied in the middle: $\boldsymbol{F}$;
  4. Predict the moment when the pendulum angle $\theta(t)=0$ after the sensor detection ends (after the data recording ends) and after the external force is applied: $t_{\text {nextzerotheta: }}$
  5. The time when the external force is applied: $t_{F_{\text {puts }}}$

The 3n+1 Problem | Learn Collatz Conjecture

The 3n+1 Problem is known as Collatz Conjecture.

Consider the following operation on an arbitrary positive integer:

The conjecture is that no matter what value of the starting number, the sequence will always reach 1.

Observe that once it reaches 1, it will do like the following oscillation

1 -> 4 -> 2 -> 1-.> 4 ->2 ....

So, we see when it converges to 1, or does it?

We will investigate the problem in certain details as much as possible with occasional exercises and some computer problems ( python ).

Let's start!

Let's start by playing with some numbers and observe what is happening actually.

We will need this frequently. So let's make a little piece of code to do this.

n = 12
print(n)
while n > 1:
    if n % 2 == 0 :
        n = n//2
        print (n)
    else:
        n = 3*n+1
        print (n)

This will give the output :

12 6 3 10 5 16 8 4 2 1

Now depending on the input of "n" you can get different sequences.

Exercise: Please copy this code and changing the input value of "n", play around with the sequences here. (Warning: Change it to python before implementing the code.) Eg: Do it for 7.

3n+1 Problem - sequence

If you observe that different numbers requires different time to converge and that is the unpredictable which makes the problem so hard.

There are in total two possibilities:

Exercise: Find out the length of the sequence for all the numbers from 1 to 100 by a computer program. I will provide you the code. Your job is to find a pattern among the numbers. 

c = 1
for n in range(2,101):
    i = n 
    while i > 1:
        if (i % 2 == 0):
            i = i//2
            c = c + 1
            if i == 1 :
                print( "The length of the sequence of {} is {}".format(n, c) )
                c = 1
        else:
            i = 3*i+1
            c = c + 1

Exercise: Consider the length of a sequence corresponding to a starting number "n' as L(n). Consider numbers of the form n = (8k+4) and n+1 = (8k+5), then find the relationship between L(n) and L(n+1). Try to observe the sequence of lengths for the numbers till 100 and predict the conjecture..

Exercise: Prove the conjecture that you discovered.

Hint:

8k+4 -> 2k+1 -> 6k+4 -> 3k+2

8k+5 -> 24k+ 16 -> 3k+2

Exercise: Prove that if n = 128k + 28, then L(n) = L(n+1) =L(n+2)

Hint:

128k+28 -> 48k+11 -> 81k+20

128k+29 -> 48k+11 -> 81k+20

128k+30 -> 81k+20

Exercise: Try to generalize the result for general k consecutive elements. Maybe you can take help of the computer to observe the pattern. Modify the code as per your choice.


You can try to do an easier problem and get the intuition as an exercise.

Exercise: Try to understand the behavior and the terminating number of the sequence if the rule is the following:

Consider the following operation on an arbitrary positive integer:


1. If the number is even, divide it by two.
2. If the number is odd, add 1.


Exercise: Try to understand the behavior and the terminating number of the sequence if the rule is the following:
Consider the following operation on an arbitrary positive integer:

1. If the number is even, divide it by two.
2. If the number is odd, add any 3.


Exercise: Try to understand the behavior and the terminating number of the sequence if the rule is the following:
Consider the following operation on an arbitrary positive integer:

1. If the number is even, divide it by two.
2. If the number is odd, add ANY ODD NUMBER.

Eager to hear your approaches and ideas. Please mention them in the comments.

Other useful links:-

Zonal Computing Olympiad 2018 Solutions-I

 Here is the part 1 of solutions of Zonal Computing Olympiad 2018 of International Informatics Olympiad  held in Tsukuba, Japan.

Problem 1: BIRTHDAY-CAKES

Before going to the solution/hints, it's always good if you re-read ( assuming you've already encountered the problem ) the problem statement once. And if you aren't aware of the problem statement, then it's only logical that you read it.
In any case, if you need to see the statement of the problem, you can find it here:

Zonal Computing Olympiad 2018 Questions.

Now, let us deal with the cases that constitute the problem. They are precisely k=0 and k=1

Case-I (k=0)
This case is pretty trivial. It can be solved with a bit of thought.
The algorithm we follow for this is:

Take each pair [a,b] denoting the permissible ranges of the cakes which a child can enjoy.
If a!=b, we append elements in range (a,b) { both inclusive } to an empty array declared beforehand.
If a==b, we append only a to the array.
Then we check if the array has any duplicate elements or not.
If it does, we print "BAD" , else we print "GOOD".

Case-II (k=1)
This case can be a lot simplified, the moment we realize the fact that INTERSECTIONS of the permissible ranges in which a child enjoys  cakes can occur only in TWO ways.
ONE way being when the destination ( last element ) of a permissible range, is equal to the source ( first element ) of another permissible range.
{ In terms of interpretation in code, we will have a function dupli_1(arr)  that returns 1 if any two consecutive elements in an array are equal. We will check if we have dupli_1(arr) = 1 for the array that contains all pairs (a,b) appended to it. }
ANOTHER way we can have fights is when an entire permissible range of cakes for some child is CONTAINED in the permissible range of cakes for another child, that is, for eg, the string "6" is 'entirely contained' in the array "567". ( In other words "6" is a substring of "567" ).

{ We use the contiguous substring concept here, and have a function dupli_2(array) that returns 1 if a string in the array is a contiguous substring of any other string in the same array.}
Now if both of the aforementioned functions return 1, we break and output "BAD" immediately, because the question gives us the liberty to move at max one child.
If anyone of those functions return 1, we act accordingly.
If dupli_1(arr)==1, we find out the particular element ; and take the minimum of the lengths of the two strings it occurs in, Assume this length to be g. Let w be the no. of elements, which are IN [1,..9] but NOT IN arr. ( These checks take linear time ).
If w >=g : we print "GOOD" , else we print "BAD"
Alternatively, if dupli_2(array)==1, we take g to be the length of the substring. And the deciding factor stays the same.

Hence, done.

Another approach to k=1:

We find any pair which intersects and let's think them to be i and i+1 and check if we can place i+1 in vacant places without overlaps via brute-force.

Zonal Computing Olympiad 2018 Questions.

These are the Questions from Zonal Computing Olympiad 2018  Exam of International Infromatics Olympiad held in Tsukuba, Japan.                                                                       

Problem 1 : BIRTHDAY-CAKES
In a birthday party, there are C cakes and N children. There is also an integer k, given.
But since eating too much of cakes can give you toothache, each of the children have been prescribed by doctors to eat cakes that fall only within a specific interval (a,b) both inclusive.

If k = 0, you have answer if any of the students' ranges clash or not.
That is print "GOOD" ( without quotes ) if ranges do not clash and "BAD" ( without quotes ) if they will fight over their share of cakes.

If k=1, then you have a chance to stop them to stop them from fighting. You are allowed to move at max 1 child from his place and allot him a different range, PROVIDED THAT HE IS STILL ABLE  TO HAVE THE SAME NUMBER OF CAKES AS HE WOULD HAVE HAD IN HIS PREVIOUS RANGE.
If you can prevent all the fights among the children, by 'moving' only one child , print "GOOD"  ( without quotes ) , else print "BAD" ( without quotes ).

Input Format

A single line containing an integer t, denoting the number of test cases.
For each test case, input 3 space separated integers denoting N, C and k
For each test cases, C lines follow, denoting the ranges within which the children can enjoy cakes.

Output Format
t lines.
Each line containing either "GOOD" or "BAD" , as applicable.

Sample Testcases

Input

3
5 2 0
2 2
3 5
5 2 1
2 2
2 5
5 2 1
2 3
2 5

Output
GOOD
GOOD
BAD

Explanation

In the second test case, the child at [2,2] can be moved to [1,1] so that there are no fights anymore. Also, note that the child can still enjoy 1 cake as he would have done, had his position not been 'moved'.

Problem 2: IMPORTANT STRINGS

After having cakes at the birthday, you've got to study some English.
You may feel strings are a random collection of characters, but no they are important, and this is how.
Suppose you have a string S of length N consisting of X, Y, and Z .
A string is 'good' if it starts with a 'X' , ends with a 'Z' and has a length divisible by 3. ( That is permissible lengths are 3, 6, 9....and so on )

The importance of a string is the number of good string it intersects with.

Given the string S and a length k, find a string of length exactly k and minimize it's importance.
Your job is to print the minimum importance.

Input Format

The first line contains a single integer t, denoting the number of test cases.
Each test case contains two lines.
The first line of each test case contains two space separated integers denoting N and k.
The second line of each test case contains the string S.

Output Format
t lines.
Each line contains a single integer denoting the required minimum importance.

Sample Testcases

Input
2
9 3
X Y Z Z Y X X Y Z
4 2
Y X Y Z

Output
1
1

Explanation
In the first testcase, the good strings are in the ranges [0,2] [0,8] and [6,8]. ( 0-based indexing has been used )
Now consider the string at [5,8]. It is of length k=3. It intersects with only one good string [0,8] ; ( the entire one ).
That's the best we can do. So it has importance 1, and that's our desired output.

You may visit this link to see the solutions:- https://cheenta.com/zonal-computing-olympiad-2018-solutions-i/