UGA

1. (A)	2. (C)	3. (B)	4. (B)	5. (A)	6. (D)
7. (D)	8. (D)	9. (B)	10. (B)	11. (C)	12. (D)
13. (C)	14. (D)	15. (B)	16. (D)	17. (D)	18. (C)
19. (C)	20. (A)	21. (A)	22. (C)	23. (B)	24. (A)
25. (C)	26. (B)	27. (A)	28. (B)	29. (D)	30. (B)

Problem 1

In the \(x y\)-plane, the curve \(3 x^3 y+6 x y+2 x y^3=0\) represents

(A) a pair of straight lines
(B) an ellipse
(C) a pair of straight lines and an ellipse
(D) a hyperbola

Solution

\(3 x^3 y+6 x y+2 x y^3=0\)

\(x y\left(3 x^2+2 y^2+6\right)=0\)

\(\Rightarrow x y=0\)

OR

\(3 x^2+2 y^2+6=0\)

no solution as \(3 x^2+2 y^2 \geqslant 0\)

\(\therefore \quad x y=0\)

\(\Rightarrow x=0\) or \(y=0\)

Answer: Pair of Straight Lines.

Problem 2

Let \(I=\int_3^5 \frac{1}{1+x^3} d x\). Then

(A) \(I<\frac{1}{64}\)

(B) \(I>\frac{1}{13}\)
(C) \(\frac{1}{63}<I<\frac{1}{14}\)

(D) \(I>\frac{1}{2}\left(\frac{1}{14}+\frac{1}{63}\right)\)

Solution

We know that

\(m(a-b) \leqslant \int_b^a p(x) d x \leqslant M(a-b)\)

Where \(m=\min . f(x)\) and

\[
B \leqslant x \leqslant a
\]

\(M=m o x \quad f(x)\)

\(b \leqslant x<a\)

So, \(2 x \frac{1}{126}<\int_3^5 f(x) d x \quad \leqslant 2 x \frac{1}{28}\)

\(\Rightarrow \frac{1}{ 63}<\int_3^5 f(x) d x<\frac{1}{14}\)

Problem 3

The coefficient of \(x^8\) in \((1-3 x)^6\left(1+9 x^2\right)^6(1+3 x)^6\) is

(A) \(-3^9 \times 5\)
(B) \(3^9 \times 5\)
(C) \(-3^8 \times 5\)
(D) \(3^8 \times 5\)

Solution:

\((1-3 x)^6\left(1+9 x^2\right)^6(1+3 x)^6\)

=\(\left(1-9 x^2\right)^6\left(1+9 x^2\right)^6\)

=\(\left(1-81 x^4\right)^6\)

\(\therefore\binom{6}{0} 1^0 \cdot\left(-81 x^4\right)^6+\cdots+\binom{6}{4} 1^4\left(-81 x^4\right)^2+\cdots\)

=\(5 \times 3^9 \times x^8\)

Problem 4

Consider two events \(A\) and \(B\) with probabilities \(P(A)\) and \(P(B)\) respectively such that \(0<P(A), P(B)<1\). Define

\[
P(A \mid B)=\frac{P(A \cap B)}{P(B)}
\]

Consider the following statements.

(I) \(P\left(A \mid B^c\right)+P(A \mid B)=1\).
(II) \(P\left(A^c \mid B\right)+P(A \mid B)=1\).

Then, in general,

(A) (I) is true and (II) is false
(B) (I) is false and (II) is true
(C) both (I) and (II) are true
(D) both (I) and (II) are false

Solution

Problem 5

Let \(f(x)=7 x^{11}+4 x^3-3\). Then \(f\) has

(A) exactly 1 real root
(B) exactly 3 real roots
(C) exactly 5 real roots
(D) 11 real roots

Solution

\(f(x)=7 x^{11}+4 x^5-3\)

\(f^{\prime}(x)=77 x^{10}+20 x^4\)

\(\therefore f^{\prime}(x)>0 \quad) if (\quad x \neq 0\)

\[
\lim_{x \to \infty} f(x) = \infty \quad \text{and} \quad \lim_{x \to -\infty} f(x) = -\infty
\]

By intermediate value theorem there is at least 1 root

\(\therefore f\) is (almost) monotone hence there is exactly 1 root.

Problem 6

Let \(A\) be an \(m \times n\) matrix with the \((i, j)\) th entry given by the real number \(a_{i j}, 1 \leq i \leq m, 1 \leq j \leq n\). Let

\[
a = \max_{1 \leq j \leq n} \left( \min_{1 \leq i \leq m} a_{ij} \right)
\quad \text{and} \quad
\beta = \min_{1 \leq j \leq n} \left( \max_{1 \leq i \leq m} a_{ij} \right).
\]

Then

(A) \(\alpha \leq \beta\) but not necessarily \(\alpha=\beta\)
(B) \(\beta \leq \alpha\) but not necessarily \(\alpha=\beta\)
(C) \(\alpha=\beta\)
(D) nothing can be said in general

Solution

Problem 7

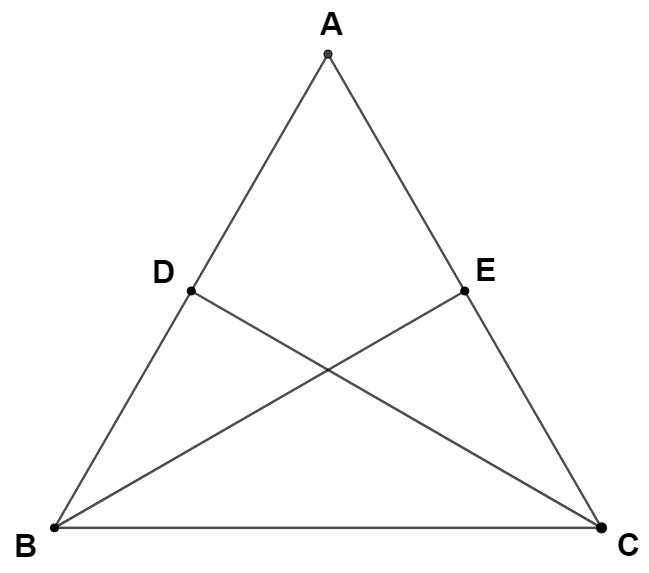
Consider the cyclic quadrilateral \(A B C D\) given below.

Assume that \(A B=B C, A D=C D\), and \(\frac{A B}{A D}=\frac{1}{3}\). Let \(\theta=\angle A D C\). Then \(\cos \theta\) is equal to

(A) \(\frac{1}{5}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{3}{5}\)
(D) \(\frac{4}{5}\)

Solution

\(x^2+x^2-2 x \cdot x \cdot \cos (180-\theta)\)

=\((3 x)^2+(3 x)^2-2 \cdot 3 x \cdot 3 x \cos \theta\)

\(\Rightarrow 2 x^2+2 x^2 \cos \theta=18 x^2-18 x^2 \cos \theta\)

\(\Rightarrow 20 x^2 \cos \theta=16 x^2\)

\(\cos \theta=\frac{16 x^2}{20 x^2}\)

=\(\frac{4}{5}\)

Problem 8

Let \(A={(x, y): x, y \in[0,1]}\) and \(B={(x, y): x, y \in[0,2]}\). Define \(f: A \rightarrow B\) by \(f(x, y)=\left(x^2+y, x+y^2\right)\). Then \(f\) is

(A) one-to-one but not onto
(B) onto but not one-to-one
(C) both one-to-one and onto
(D) neither one-to-one nor onto

Solution

\(A={(x, y): x, y \in[0,1]}\)

\(B={(x, y): x, y \in[0,2]}\)

\(f: A \rightarrow B\)

\(f(x, y)=\left(x^2+y ; x+y^2\right)\)

Not one -on - one

as \(\begin{array}{r}(1,0) \ (0,1)\end{array}\) --> both map to \((1,1)\)

Onto, Examina the presimage of \([0,2]\)

\(x^2+y=0\)

\(x+y^2=2\).

\(\because \quad 0 \leqslant x, y \leqslant 1\)

\(\therefore x^2+y=0 \Rightarrow \quad x=0 \quad y=0\)

But then \(x+y^2=2\) is not true hence no solution.

Problem 9

The number of ordered pair \((a, b)\) of positive integers with \(a<b\) satisfying \(a^2+b^2=2025\) is

(A) 0
(B) 1
(C) 2
(D) 6

Solution

\(a^2+b^2=2.25\)

\(a<b\)

\(\therefore \quad 2025=5^2 \cdot 3^4=45^2\)

\(0,1,4,7 \quad \bmod 9\)

None of these work except \(0+0\)

\(\therefore \quad a^2 \equiv 0 \mathrm{mod} 9\)

\(b^2 \equiv 0\) mod 9

\(\therefore a \leq 0 \bmod a\)

or \(a \equiv 6 \bmod 9\).

\(\therefore\) Both a and 6 are divisible by 3

\(\left(3 a_1\right)^2+\left(3 b_1\right)^2=25 \times 81\)

\(\Rightarrow a_1^2+b_1^2=9 \times 25\)

\(\Rightarrow \quad a_2{ }^2+b_2{ }^2=25\)

\(\therefore a_2=3, b_2=9\)

\(\therefore a=27 \quad b=36\)

Problem 10

Twelve boxes are placed along a circle. In each box, \(1,2,3\) or 4 balls are put such that the total number of balls in any 4 consecutive boxes is same. The number of ways this can be done is

(A) 4 !
(B) \(4^4\)
(C) \((4!)^3\)
(D) \((4!)^4\)

Solution

once we choose number of balls in first 4 boxes, the remaining choices become fixed.

For each of the four boxes, we have four choices,

\(\therefore 4^4\) cases in total

Problem 11

Let \(a_0=0, a_1=1\) and \(a_n=5 a_{n-1}+a_{n-2}\) for \(n \geq 2\). Then the value of the determinant

is

(A) -1
(B) \(-5^{101}\)
(C) 1
(D) \(5^{101}\)

Solution

Problem 12

The lengths of the three sides of a right angled triangle are geometric progression. The smallest angle of the triangle is

(A) \(\tan ^{-1}\left(\frac{\sqrt{5}-1}{2}\right)\)
(B) \(\cos ^{-1}\left(\frac{2}{\sqrt{5}-1}\right)\)
(C) \(\sin ^{-1}\left(\frac{2}{\sqrt{5}-1}\right)\)
(D) \(\sin ^{-1}\left(\frac{\sqrt{5}-1}{2}\right)\)

Solution

Problem 13

Consider the following statements about two similar triangles \(\Delta_1), and (\Delta_2\).

\(S_1\): Lengths of the sides of \(\Delta_1\) are in arithmetic progression
\(S_2\). Lengths of the sides of \(\Delta_1\) are in geometric progression.

\(S_3\). Lengths of the sides of \(\Delta_2\) are in arithmetic progression.

\(S_4\). Lengths of the sides of \(\Delta_2\) are in geometric progression.

Then

(A) \(S_1\) implies \(S_3\), but \(S_2\) does not imply \(S_4\)
(B) \(S_1\) does not imply \(S_3\), but \(S_2\) implies \(S_4\)
(C) \(S_1\) implies \(S_3\), and \(S_2\) implies \(S_4\)
(D) \(S_1\) does not imply \(S_3\), and \(S_2\) does not imply \(S_4\)

Solution

Let \((\sigma, b, c)\) and \(\left(a^{\prime}, b^{\prime}, c^{\prime}\right)\) are

Sides of two similar triangles sit.

\(\frac{a}{a^{\prime}}=\frac{b}{b^{\prime}}=\frac{c}{c^{\prime}}\)

and \(b=a r\) and \(a-a x^2\)

Ther, \(\frac{b^{\prime}}{a^{\prime}}=\frac{c\prime}{b\prime}=r\) also

So, \(S_2\) implips \(S_4\)

Now, let

\(b=a+d\) \(c=a+d\)

so, \(a^{\prime}: a k, b^{\prime}:(a+d) k\).

So, \(a^{\prime}, b^{\prime}, c^{\prime}\), are also in AP

so, \(S_2\) implies \(S_4\)

Problem 14

For each \(n \geq 1\), let \(a_n\) and \(b_n\) be real numbers such that \(a_n \neq 0\) \(\frac{a n d}{c} b_n \neq 0\). Let

\(\left(a_n+i b_n\right)^n=n\left(a_n+i b_n\right) \quad\) for all \(n \geq 6\).

Then

(A) no such (a_n, b_n) exist
(B) \(x_n=n^{\frac{1}{n+1}} \cos \frac{2 \pi}{n+1}, b_n=n^{\frac{1}{n+1}} \sin \frac{2 \pi}{n+1}\)
(C) \(a_n=n^{\frac{1}{n}} \cos \frac{2 \pi}{n}, b_n=n^{\frac{1}{n}} \sin \frac{2 \pi}{n}\)
(D) \(a_n=n^{\frac{1}{n-1}} \cos \frac{2 \pi}{n-1}, b_n=n^{\frac{1}{n-1}} \sin \frac{2 \pi}{n-1}\)

Solution

\(\left(a_n+i \cdot b_n\right)^n=n\left(a_n+i \cdot b_n\right)\).

\(\Rightarrow\left(a_n+i \cdot b_n^m\right)^{n-1}=n\).

As, \(\quad a_n+i b_n \neq 0\)

So, \(a_n+i b_n=\)

\(\frac{1}{n-1}\left[\cos \left(\frac{2 \pi k}{n-1}\right)\right.\) \(fi (\sin \left(\frac{2 \pi k}{n-1}]\right)\)

where \(0 \leqslant K<(n-1)\)

So, option (D)

Problem 15

The lengths of the two adjacent sides of a parallelogram are 2 cm and 3 cm . The length of one diagonal is \(\sqrt{19} \mathrm{~cm}\). Then the length of the other diagonal is

(A) \(\sqrt{5} \mathrm{~cm}\)
(B) \(\sqrt{7} \mathrm{~cm}\)
(C) \(\sqrt{15} \mathrm{~cm}\)
(D) \(\sqrt{21} \mathrm{~cm}\)

Solution

\(d_1^2=a_b^2+b_b^2-2 a b \cos \theta\)

\(d_2^2=a^2+b^2-2 a b \cos \left(180^{\circ}-\theta\right)\)

\(\therefore d_1^2+d_2^2=2\left(a^2+b^2\right)\)

\(\Rightarrow 19+d_2^2=2(4+9)\)

\(\Rightarrow \quad d_2^2=26-19 \Rightarrow d_2^2=7\)

\(=d_2=\sqrt{7}\)

Problem 16

Let \(f\) \((x) = \frac{1}{1+|x-1|}+\frac{1}{1+|x+1|}\). Then the function \(f\) has
(A) neither a local maximum nor a local minimum
(B) a local minimum at \(x=0\), but no local maximum
(C) local maxima at \(x= \pm 1\), but no local minimum
(D) a local minimum at \(x=0\) and local maxima at \(x= \pm 1\)

Solution

\(f(x)=\frac{1}{1+|x-1|}+\frac{1}{1+|x+1|}\)

when, \(x<-1\),

\(f(x)=\frac{1}{2-x}-\frac{1}{x} \Rightarrow f^{\prime}(x)=\frac{1}{(2-x)^2}+\frac{1}{x^2}>0\)

Hence, (f(x)) is increasing

\(f(x)=\frac{1}{x+2}+\frac{1}{2-x} \Rightarrow f^{\prime}(w)=\frac{1}{(2-w)^2}-\frac{1}{(x+2)^2}\)

Critical point, at \(x=0\)

\(f^{\prime}(n)>0) for (0 \leqslant n<1\).

\(f^{\prime}(x)<0) for (-1<x<0\)

when, \(n>1\).

\(f(n)=\frac{1}{n}+\frac{1}{n+2}\)

\(=-\frac{1}{n^2}-\frac{1}{(n+2)^2}<0\)

\(f(x)\) is decreasing.

at \(x= \pm 1 \quad f(x)\) is changing it's sign from positive to

& at \(x=0\) it is changing from negative to positive.

Hence, option (D)

Problem 17

\(f(x) =
\begin{cases}
-1, & \text{if } x < 0,
\ 0, & \text{if } x = 0,
\ 1, & \text{if } x > 0.
\end{cases}\)

Then the function \(F\) defined by \(F(x)=\int_{-5}^x f(t) d t\) is

(A) not continuous
(B) continuous, but nowhere differentiable
(C) differentiable everywhere
(D) differentiable everywhere except at 0

Solution

Problem 18

Let
\(L=\lim _{n \rightarrow \infty}(n+100)^{\frac{5}{5 g_e(n-50)}}\).
Then
(A) \(2 \leq L \leq 16\)
(B) \(16 \leq L \leq 32\)
(C) \(32 \leq L<243\)
(D) \(L>243\)

Solution

\(L=\lim _{n \rightarrow \infty}(n+100) \frac{5}{\ln (n-\infty)}\)

\(\Rightarrow \ln L=\frac{5 \ln (n+100)}{\left.\lim _{n \rightarrow \infty} \frac{\ln (n-50)}{\ln (n-5}\right)}=5\)

\(L=e^5\)

\(2<e<3\)

\(32<L<243\)

Problem 19

Let \(a, b, c, d\) be positive integers such that the product abcd (=999). Then the number of different ordered 4 -tuples \((a, b, c, d)\) is

(A) 20
(B) 48
(C) 80
(D) 84

Solution

\(999=3^3 \times 27\)

Hence the number of non-negetive integer solution

\(\binom{3+4-1}{4-1}\binom{1+4-1}{4-1}\)

\(=20 \times 4\)

\(=80\)

Problem 20

Let \(|x|\) denote the greatest integer less than or equal to \(x \in \mathbb{R}\) and \(|x|\) has its usual meaning, that is, \(|x|=x\) if \(x \geq 0\), and \(|x|=-x\), if \(x<0\). Then the value of the integral

\(\int_{-2}^1([x]+2)^{|x|} d x\)

is
(A) \(1+\frac{1}{\log _e 2}\)
(B) \(1+\log _e \frac{1}{2}\)
(C) \(2-\log _e 2\)
(D) none of the above

Solution

\(\int_{-2}^1([x]+2)^{|x|} d x\)

\(=\int_0^1 2^x d x+\int_{-1}^0 1^{-x} d x\)

\(f \int_{-2}^{-1} 0 \cdot d x\)

\(=\left[\frac{2 x}{\ln 2}\right]_0^1+1.1\)

\(\left(\frac{1}{\ln^2}+1\right)\)

Problem 21

For a real number \(x\), let \(f(x)=\int_{-20}^{20} g(t) g(x-t) d t\), where
\(g(x)= \begin{cases}1, & \text { if } x \in[0,1] \ 0, & \text { otherwise }\end{cases}\)

Then \(f(x)\) is equal to
(A) \(\begin{cases}x, & \text { if } x \in[0,1], \ 2-x, & \text { if } x \in[1,2], \ 0, & \text { otherwise }\end{cases}\)
(B) \(\begin{cases}1+x, & \text { if } x \in[0,1), \ 1-x, & \text { if } x \in[1,2), \ 0, & \text { otherwise }\end{cases}\)
(C) \(\begin{cases}1, & \text { if } x \in(-20,20), \ 0, & \text { otherwise }\end{cases}\)
(D) none of the above

Solution

Now, if \(x<0\) or \(x>2\)then the integration becomes 0 .

if \(\quad 0 \leq x \leq 1\)

Then \(f(x)\)

\(=\int_{x-1}^x g(t) d t\)

\(=\int_0^x d t=x\)

\(=\int_{-20}^{20} \theta(t) g(x-t) d t\)

\(=\int_0^1 g(x-t) d t\)

\(=\int_0^1 g(t+x-1) d t\)

\(=\int_{x-1}^x g(t) d t\)

it \(10 \leqslant x \leqslant 2\)

\(f(x): \int_{x-1}^x g(t) d t\)

\(=\int_{x-1}^1 d t=(2-x)\)

Problem 22

Let \(n \geq 3\). There are \(n\) straight lines in a plane, no two of which are parallel and no three pass through a common point. Their points of intersection are joined. Then the number of fresh line segments thus created is
(A) \(\frac{n(n-1)(n-2)}{8}\)
(B) \(\frac{n(n-1)(n-2)(n-3)}{6}\)
(C) \(\frac{n(n-1)(n-2)(n-3)}{8}\)
(D) none of the above

Solution

The lines intersect at \(\binom{n}{2}\) different points But there are also \((n-1)\) points in part of line

So, Total fresh line

\(=\binom{\binom{n}{2}}{2}-n\binom{n-1}{2}\)

\(=\left(\frac{n(n-1)}{2}\right)-n \cdot \frac{(n-1)(n-2)}{2}\)

\(=\frac{n(n-1)(n-2)(n+1)}{8}-\frac{n(n-1)(n-2)}{2}\)

\(=\frac{n(n-1)}{8} \cdot\left(n^2-n-2-4 n+\theta\right)\)

\(=\frac{n(n-1)(n-2)(n-3)}{8}\)

Problem 23

In a certain test there are \(n\) questions. At least \(i\) questions were wrongly answered by \(2^{n-i}\) students, where \(i=1,2, \ldots, n\). If the total number of wrong answers given by all students is 2047 , then (n) is equal to
(A) 10
(B) 11
(C) 12
(D) 13

Solution

At least \(i\) questions were wrongly answered by \(2^{n-i}\) students.

\(\therefore\) At least wrong answers

\(=\) Exactly \(n-3\) wrong answers +

Exactly \(n-2\) wrong answers+

Exactly \(n-1\) wrong answers+

Exactly \(n\) wrong answers

\(\therefore\) Exactly: questions wrong \(=2^{n-1}-2^{n-2}\) Exactly 2 questions wrong \(=2^{n-2}-2^{n-3}\)

\(\therefore\) Total number of wrongs

\[
\begin{aligned}
& 1\left(2^{n-1}-2^{n-2}\right)+2\left(2^{n-2}-2^{n-3}\right)+\cdots+n\left(2^1-2^0\right) \
& =2^{n-1}+2^{n-2}+2^{n-3}+\cdots+2^1+2^0
\end{aligned}
\]

\(\therefore 2^0+2^1+2^2+\cdots+2^{n-3}+2^{n-2}+2^{n-1}=2047\)

\(\Rightarrow \frac{2^0\left(2^n-1\right)}{2-1}=2047\)

\(\Rightarrow \quad 2^n-1=2047 \Rightarrow n=11\)

Problem 24

Let \(n\) be a positive integer. The value of \(\sum_{k=0}^n \tan ^{-1} \frac{1}{k^2+k+1}\) is
(A) \(\tan ^{-1}(n+1)\)
(B) \(\tan ^{-1}\left(\frac{1}{n+1}\right)\)
(C) \(\tan ^{-1} n\)
(D) \(\tan ^{-1}\left(\frac{1}{n}\right)\)

Solution

\(=\sum_{k=0}^n \tan ^{-1} \frac{1}{k^2+k+1}\)

\(=\sum_{k=0}^n \tan ^{-1} \frac{1}{k(k+1)+1}\)

\(=\sum_{k=0}^n \tan ^{-1} \frac{(k+1)-k}{k(k+1)+1}\)

\(=\sum_{k=0}^n\left[\tan ^{-1}(k+1)-\tan ^{-1}(k)\right]\)

\(=\tan ^{-1}(n+1)\)

Problem 25

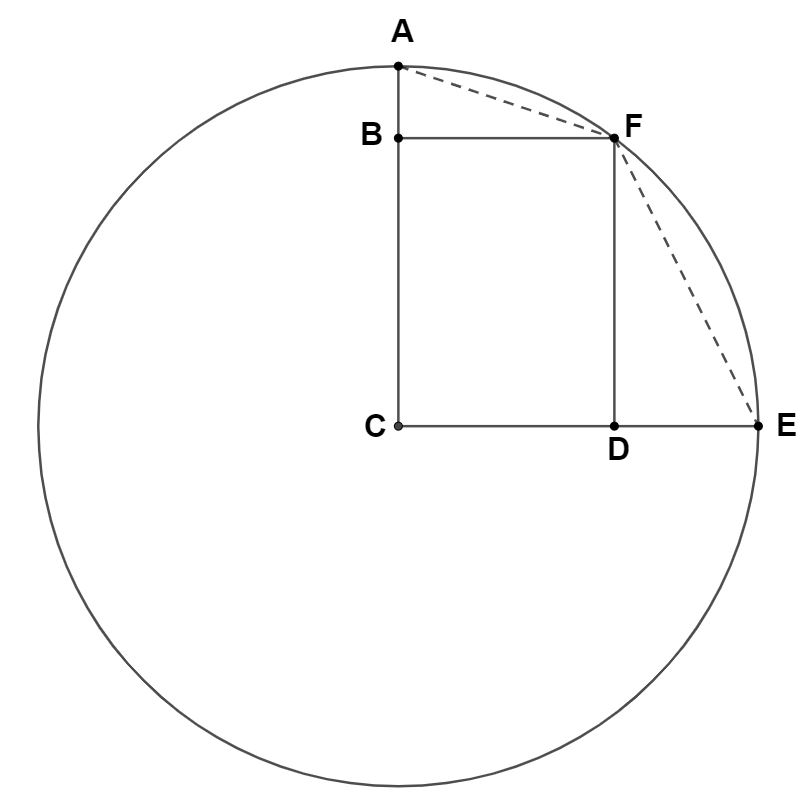
Let \(d\) be the side length of the largest possible equilateral triangle that can be put inside a square of side length 1 . Then
(A) \(d<1\)
(B) \(d=1\)
(C) \(1<d<\frac{2}{3^{1 / 4}}\)
(D) \(d \geq \frac{2}{3^{1 / 4}}\)

Problem 26

Let \(f(x)=\left(x^2+18\right)(x-4) x(x+4)-2\). Then
(A) \(f\) has exactly one real root
(B) \(\int\) has exactly 3 distinct real roots
(C) \(f\) has 5 distinct real roots
(D) \(f\) has a repeated root

Solution

\(f(x)=\left(x^2+18\right) x(x-4)(x+4)-2\)

\(f^{\prime}(x)=5 x^4+6 x^2-288\)

\(f^{\prime}\) has two real roots

But \(f\) can have at most three real roots. But \(f(-4)<0 \quad f(-3)>0 \quad f(0)<0 \quad f(4)<0 \quad f(5)>0\)

\( \therefore \) it has 3 real roots (B).

Problem 27

Yet \(k\) be a positive integer and \(f(x)=e^x-1\). Then

\[\lim _{x \rightarrow 0} \frac{f(x)+f\left(\frac{x}{2}\right)+f\left(\frac{x}{2^2}\right)+\cdots+f\left(\frac{x}{2^k}\right)}{x}\]

(x) \(2-\frac{1}{2^k}\)
(B) \(2-\frac{1}{2^{k+1}}\)
(C) \(k\)
(D) \(2^{k+1}-1\)

Solution

\(f(x)=e^x-1\)

\(\lim _{x \rightarrow 0} \frac{e^x-1}{x}+\frac{e^{x / 2}-1}{x}+\frac{e^{x / 2^2}-1}{x}+\cdots+\frac{e^{x / 2^x}-1}{x}\)

\(=\lim _{x \rightarrow 0} \frac{e^x-1}{x}+\frac{e^{x / 2}-1}{x / 2} \times \frac{1}{2}+\frac{e^{x / 2^2}-1}{x / 2^2} \times \frac{1}{2^2}+\cdots+\frac{e^{x / 2^x}-1}{x / 2^x} \times \frac{1}{2^x}\)

=\(1+\frac{1}{2}+\frac{1}{2^2}+\cdots+\frac{1}{2^x}=-\frac{1\left(\frac{1}{2^{x+1}}-1\right)}{1 / 2}\)

\(=-2\left(\frac{1}{2^{x+1}}-1\right)\)

\(=-\left(\frac{1}{2^k}-2\right)=2-\frac{1}{2^k}\)

Problem 28

Let

\[a_n=\frac{n^2}{\sqrt{n^6+1}}+\frac{n^2}{\sqrt{n^6+2}}+\cdots+\frac{n^2}{\sqrt{n^6+n}}, \quad n \geq 1\]

Then \(\lim _{n \rightarrow \infty} a_n\)
(A) does not exist
(B) is equal to 1
(C) is equal to \(e\)
(D) is equal to \(\frac{1}{e}\)

Solution

\(a_n=\frac{n^2}{\sqrt{n^6+1}}+\frac{n^2}{\sqrt{n^6+2}}+\cdots+\frac{n^2}{\sqrt{n^6+n}}\)

\(\sqrt{n^6+0} \leq \sqrt{n^6+r} \leq \sqrt{n^6+n}\)\

\(\frac{1}{\sqrt{n^6}} \leqslant \frac{1}{\sqrt{n^6+r}} \leqslant \frac{1}{\sqrt{n^6+n}}\)

\(\frac{n^2}{n^3}-\leqslant \frac{n^2}{\sqrt{n^6+r}} \leqslant \frac{n^2}{\sqrt{n^6+n}}\)

\(\sum_{r=1}^n \frac{n^2}{n^3} \leqslant \sum_{r=1}^n \frac{n^2}{\sqrt{n^6+r}} \leqslant \sum_{n=1}^n \frac{n^2}{\sqrt{n^6+n}}\)

\(\frac{n^3}{n^3} \leqslant \sum_{r=1}^n \frac{n^2}{\sqrt{n^6+r}} \leqslant \frac{n^3}{\sqrt{n^6+n}}\)

\(1 \leqslant \sum_{r=1}^n \frac{n^2}{\sqrt{n^6+r}} \leqslant \frac{n^{B^3}}{\sqrt{n^6+n}}\)

\[
1 \leq \lim_{n \to \infty} \sum_{r=1}^{n} \frac{n^2}{\sqrt{n^6 + r}} \leq 1 = \lim_{n \to \infty} \frac{n^3}{\sqrt{n^6 + n}}
\]

So, \(\lim _{n \rightarrow \infty} a_n=1\)

Problem 29

A subset ${u_1, u_2, u_3, u_4, u_5}$ of the first 90 positive integers can be selected in $\binom{90}{5}$ ways. Let $u_{\text{max}} = \max{u_1, u_2, u_3, u_4, u_5}$ and $u_{\text{min}} = \min{u_1, u_2, u_3, u_4, u_5}$. Then the arithmetic mean of $u_{\text{max}} + u_{\text{min}}$ over all such subsets is

(A) 45
(B) 46
(C) 89
(D) 91

Solution

No. of subsets whose max element 90 is \(\quad 90\binom{89}{4}\)

When \(u_{\text {max }}=89 \rightarrow 89\binom{88}{4}\)

When \(u_{\text {max }}^{\text {max }}=88 \rightarrow 88\binom{87}{4}\)

" " "

" " "

" " "

when \(u_{\max }=5 \rightarrow 5\binom{4}{4}\)

Now, when \(u_{\min }=1 \rightarrow 1\binom{89}{4}\).

when \(u_{\min }^{\min }=2 \rightarrow 2\binom{88}{4}\)

when \(u_{\text {min }}=3 \rightarrow 3\binom{87}{4}\)

" " "

" " "

when \(u_{\min }=86 \rightarrow 86\binom{4}{4}\)

\(\therefore\) Sum of all possible values

\(90\binom{89}{4}+89\binom{88}{4}+\left(88\binom{87}{4}+\cdots+5\binom{4}{4}\right.\)

\(+1\binom{89}{4}+2\binom{88}{4}+\cdots+86\binom{4}{4}\)

\(=91\left[\binom{89}{4}+\binom{88}{4}+\binom{87}{4}+\cdots+\binom{4}{4}\right]\)

\(=91\binom{90}{5} \quad\) [Hockey-Stick Identity]

\(\therefore A M\) of all \(u_{\text {max }}+u_{\text {min }}=\frac{91\binom{90}{5}}{\binom{90}{5}}\)

\(=91\)

Problem 30

Let

\[a_n=\frac{2^3-1}{2^3+1} \times \frac{3^3-1}{3^3+1} \times \cdots \times \frac{n^3-1}{n^3+1}, \quad n \geq 2\]

Then \(\lim _{n \rightarrow \infty} a_n\)
(A) does not exist
-(B) is equal to \(\frac{2}{3}\)
(C) is equal to 1
(D) is equal to \(\frac{1}{2}\)

Solution

\(\frac{r^3-1}{r^3+1}=\frac{r-1}{r+1} \times \frac{r^2+r+1}{r^2-r+1}\)

\(\left(\frac{r-1}{r+1}\right) \times \frac{(r+1)^2-(r+1)+1}{\left(r^2-r+1\right)}\)

\(\prod_{r=2}^n\left(\frac{r-1}{r+1}\right) \prod_{r=2}^n \frac{(r+1)^2-(r+1)+1}{r^2-r+1}\)

\(\prod_{r=2}^n\left(\frac{r-1}{r+1}\right)=\frac{1}{3} \times \frac{2}{4} \times \frac{8}{5} \times \frac{4}{6} \times \frac{5}{7} \times \frac{8}{8} \cdots=i\)

\(\prod_{r=2}^n \frac{(r+1)^2-(r+1)+1}{r^2-r+1}=\frac{3^2-3+1}{2^2-3+1} \times \frac{4^2-4+1}{3^2-3+1} \times \frac{5^2-5+1}{4^2-4+1} \times \cdots\)

= \(\frac{1}{4-2+1}=\frac{1}{3}\) (ii)

So from (i) and (ii) we get \(\frac{2}{3}\)

UGB

Problem 1

Suppose \(f: \mathbb{R} \rightarrow \mathbb{R}\) is differentiable and \(\left|f^{\prime}(x)\right|<\frac{1}{2}\) for all \(x \in \mathbb{R}\). Show that for some \(x_0 \in \mathbb{R}, f\left(x_0\right)=x_0\).

Solution

Problem 2

If the interior angles of a triangle (A B C) satisfy the equality,

\[
\sin ^2 A+\sin ^2 B+\sin ^2 C=2\left(\cos ^2 A+\cos ^2 B+\cos ^2 C\right)
\]

prove that the triangle must have a right angle.

Problem 3

Suppose \(f:[0,1] \rightarrow \mathbb{R}\) is differentiable with \(f(0)=0\). If \(\left|f^{\prime}(x)\right| \leq f(x)\) for all \(x \in[0,1]\), then show that \(f(x)=0\) for all \(x\).

Problem 4

Let \(S^1={\{z \in \mathbb{C}| | z \mid=1}\}\) be the unit circle in the complex plane. Let Let \(f: S^1 \rightarrow S^1\) be the map given by \( f(z)=z^2 \). We define \(f^{(1)}:=f\) and \(f^{(k+1)}:=f \circ f^{(k)}\) for \(k \geq 1\). The smallest positive integer \(n\) such that \(f^{(n)}(z)=z\) is called the period of \(z\). Determine the total number of points in \(S^1\) of period 2025.
(Hint: \(2025=3^4 \times 5^2) \)

Problem 5

Let \(a, b, c\) be nonzero real numbers such that \(a+b+c \neq 0\). Assume that

\[
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}
\]

Show that for any odd integer \(k\),

\[
\frac{1}{a^k}+\frac{1}{b^k}+\frac{1}{c^k}=\frac{1}{a^k+b^k+c^k}
\]

Problem 6

Let \(\mathbb{N}\) denote the set of natural numbers, and let \(\left(a_i, b_i\right)\), \(1 \leq i \leq 9\), be nine distinct tuples in \(\mathbb{N} \times \mathbb{N}\). Show that there are three distinct elements in the set \({2^{a_i} 3^{b_i}: 1 \leq i \leq 9}\) whose product is a perfect cube.

Problem 7

Consider a ball that moves inside an acute-angled triangle along a straight line, until it hits the boundary, which is when it changes direction according to the mirror law, just like a ray of light (angle of incidence (=) angle of reflection). Prove that there exists a triangular periodic path for the ball, as pictured below.

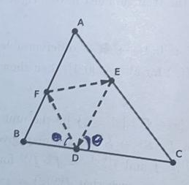
Problem 8

Let \(n \geq 2\) and let \(a_1 \leq a_2 \leq \cdots \leq a_n\) be positive integers such that \(\sum_{i=1}^n a_i=\Pi_{i=1}^n a_i\). Prove that \(\sum_{i=1}^n a_i \leq 2 n\) and determine when equality holds.